| Natureduca - Portal educativo de ciencia y cultura |

Física
ELECTRICIDAD
Circuitos de corriente continua - 20ª parte
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Circuitos serie-paralelo (continuación)
Segunda ley de Kirchhoff (continuación)
Utilizando la 2ª ley de Kirchhoff en circuitos cerrados
 e han resuelto hasta ahora, utilizando la 2ª Ley de Kirchhoff,
diversos problemas en partes aisladas de un circuito, pero tenemos que saber que también puede ser aplicada a
circuitos cerrados. En este caso, la 2ª ley puede redefinirse de la siguiente
forma: "La suma algebraica de todas las fuerzas electromotrices (f.e.m.) y
caídas de tensión alrededor de un lazo cerrado es igual a cero".
e han resuelto hasta ahora, utilizando la 2ª Ley de Kirchhoff,
diversos problemas en partes aisladas de un circuito, pero tenemos que saber que también puede ser aplicada a
circuitos cerrados. En este caso, la 2ª ley puede redefinirse de la siguiente
forma: "La suma algebraica de todas las fuerzas electromotrices (f.e.m.) y
caídas de tensión alrededor de un lazo cerrado es igual a cero".
Para comprender este concepto, tenemos que aprender primero cómo se comportan las fuentes de alimentación en un circuito, y también cómo identificar la dirección de la corriente.
Si en el circuito hay más de una fuente, entonces la tensión aplicada al mismo depende de que las fuentes se sumen o se resten (si las fuentes están conectadas en oposición se restan, y si están conectadas directamente se suman).
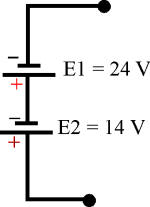
En este ejemplo las
fuentes están conectadas directamente, sus voltajes se suman:
Et = E1 + E2 = 24 + 14 = 38 voltios
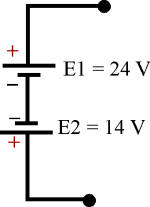
En este ejemplo las
fuentes están conectadas en oposición, sus voltajes se restan:
Et = E1 - E2 = 24 - 14 = 10 voltios
Identificando la dirección de la corriente en un circuito con varias fuentes
Identificar la dirección de la corriente es fundamental para resolver las incógnitas en circuitos serie-paralelo aplicando la 2ª Ley de Kirchhoff.
Consideremos un circuito compuesto por cuatro fuentes de diferentes valores, unas conectadas directamente y otras en oposición. Si las fuentes estuviesen todas conectadas directamente, la dirección de la corriente sería identificable a simple vista, sólo comprobando qué polo es el de signo negativo (-), ya que desde él saldría la corriente en dirección al polo positivo (+).
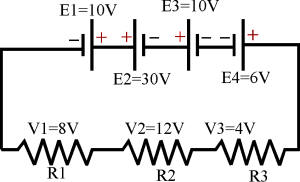
Primero tenemos que averiguar qué fuentes predominan, y esas serán las que marquen la dirección de la corriente. Para ello, sumamos independientemente todas las que están conectadas en un sentido, y después las conectadas en sentido contrario.
Así, tenemos por un lado E1 y E4:
E1 + E4 = 10 +6 = 16 voltios
Y tenemos por otro lado E2 y E3:
E2 + E3 = 30 +10 = 40 voltios
Se observa que la mayor tensión es proporcionada por E2 y E3, por tanto el sentido de la corriente es desde los polos negativos (-) de E2 y E3 hacia la resistencia R3.
Identificando la polaridad de los elementos de un circuito
Conocida la dirección de la corriente, ahora tenemos que identificar y marcar el punto de entrada y salida de la corriente en cada uno de los elementos del circuito. La regla de flujo de corriente en un circuito es que produce una carga negativa en el lado por donde entra, y una carga positiva en el lado por donde sale. Dado que en el esquema propuesto la corriente circula en dirección a R3, pondremos un signo menos en la entrada de R3 y un signo más en su salida. El mismo proceso rige para R2 y R1 que se encuentran en el camino de la corriente, y las marcaremos por tanto de igual forma con un - y un + respectivos.

Ahora, vamos a confirmar el enunciado de la 2ª Ley de Kirchhoff aplicada a circuitos cerrados. Comenzamos por cualquier punto del circuito siguiendo el sentido de la corriente, por ejemplo por R3, y vamos anotando el signo de entrada en cada elemento del circuito y su correspondiente valor de voltaje o caída de tensión, para finalmente igualarlo todo a cero:
-V3 - V2 -V1 -E1 +E2 +E3 -E6 = 0
-4 -12 -8 -10 +30 +10 -6 = 0
Si hemos aplicado bien los signos, la suma algebraica de todos estos valores será igual a cero, lo cual significa que todas las caídas de tensión en el circuito se compensan en la misma igualdad con la fuente. Esto viene a confirmar la 2ª Ley de Kirchhoff.
Con lo aprendido, ya podemos resolver un problema de una incógnita en un circuito aplicando esta regla. Tomemos como ejemplo el mismo circuito anterior, y supongamos que ignoramos el valor de V2.
Aplicamos la regla, anotando todos los valores conocidos con sus correspondientes signos, y despejamos la incógnita V2. Nuevamente la Ley se confirma:
-4 -V2 -8 -10 +30 +10 -6 = 0
V2 = -4 -8 -10 +30 +10 -6 = 12 voltios



