---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Circuitos serie-paralelo

Introducción

os circuitos serie-paralelo son combinaciones de resistencias (tres o más), una parte de las cuales están dispuestas en serie y otra parte en paralelo.

Existen dos tipos básicos de circuitos serie-paralelo: uno que incluye una resistencia en serie con una agrupación de resistencias en paralelo, y otro consistente en una agrupación de resistencias en paralelo que incluye alguna rama de resistencias en serie.

Muchos de estos circuitos son utilizados a menudo en motores eléctricos y dispositivos eléctricos de control.

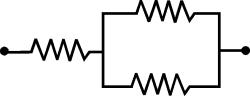
Tipo consistente en una resistencia en serie con una agrupación de resistencias en paralelo

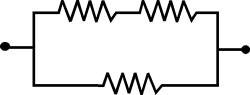
Tipo consistente en una agrupación de resistencias en paralelo, una de cuyas ramas incluye resistencias en serie

Cómo se halla la resistencia total en un circuito serie-paralelo

Para hallar la resistencia total de un circuito serie-paralelo no es necesario utilizar ninguna fórmula nueva, o diferente a las que ya conocimos por lo estudiado anteriormente en los respectivos circuitos serie y circuitos paralelo.

En realidad, un circuito serie-paralelo no es más que una combinación de ambos, por ello solo es necesario descomponerlo en sus formas más simples (serie o paralelo) y resolverlos por separado.

Simplificando los circuitos

Ejemplo A

Consideremos un circuito serie-paralelo tipo básico, compuesto por una resistencia (R1) de 10 ohmios, en serie con una agrupación en paralelo (R2 y R3) de 30 y 20 ohmios, respectivamente.

Lo primero es combinar las ramas en paralelo para obtener su resistencia equivalente, que llamaremos Ra, para a continuación sumarla con la resistencia en serie R1.

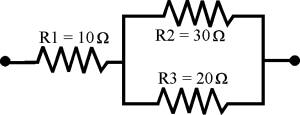
Para calcular la resistencia equivalente (Ra) de R2 y R3, podemos utilizar el método de productos entre sumas, ya estudiado en su momento (si ambas resistencias fuesen del mismo valor, sería suficiente con dividir el valor de una de ellas entre 2).

Ya sabemos que la resistencia equivalente (Ra) de las ramas en paralelo es 12 ohmios. Como se puede observar en el esquema, hemos reducido el circuito a dos simples resistencias en serie: R1 de 10 ohmios, y Ra de 12 ohmios. Por tanto, dado que en los circuitos en serie las resistencias se suman para obtener el valor total (Rt), resulta:

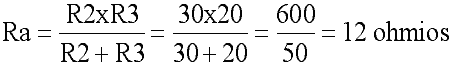
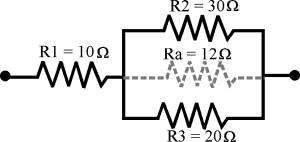
Rt = R1 + Ra = 10 + 12 = 22 ohmios

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios