/natureduca/fisica-electricidad-circuitos-de-corriente-continua-16

---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Circuitos serie-paralelo (continuación)

Cómo se halla la resistencia total en un circuito serie-paralelo (continuación)

Simplificando los circuitos (continuación)

Ejemplo B

onsideremos el otro tipo de circuito básico serie-paralelo, compuesto por una agrupación de resistencias en paralelo (R1, R2 y R3) de 50, 30 y 20 ohmios, respectivamente, una de cuyas ramas está constituida por dos resistencias en serie (R2 y R3).

El proceso es similar al ejemplo "A" explicado en la página anterior. Se trata de simplificar el circuito a una de sus formas más simples (serie o paralelo). En dicho ejemplo "A", por la naturaleza del tipo serie-paralelo de que se trata, quedó simplificado a un circuito simple "serie". En este tipo que vamos a resolver ahora, veremos que quedará simplificado a un circuito simple "paralelo".

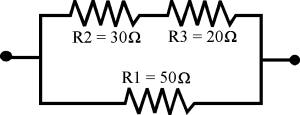
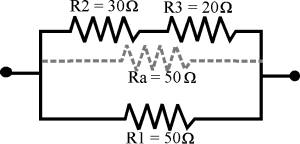
Lo primero es sumar las resistencias en serie R2 y R3, que llamaremos Ra, para a continuación combinarla con la resistencia en paralelo R1.

Ra = R2 + R3 = 30 + 20 = 50 ohmios

El circuito ha quedado reducido a dos simples resistencias en paralelo, Ra y R1, ambas de 50 ohmios cada una. Ya sólo queda utilizar alguna de las fórmulas conocidas para calcular la resistencia total de varias dispuestas en paralelo. En este caso resulta incluso más sencillo, pues ambas resistencias Ra y R1 son del mismo valor, por tanto es suficiente con tomar el valor de una (50) y dividirla entre el número de ellas (2). Así, resulta:

Conclusiones

Lo visto en ambos ejemplos A y B, sirve para cualquier tipo de circuito serie-paralelo por muy complejo que sea. Se simplifica siempre el circuito, descomponiéndolo hasta reducirlos a sus formas más simples (serie o paralelo), como se explicó, y después se calcula por separado cada circuito serie o paralelo correspondiente, utilizando los métodos y fórmulas adecuadas a cada caso.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios