/natureduca/fisica-electricidad-circuitos-de-corriente-continua-19

---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Circuitos serie-paralelo (continuación)

Segunda ley de Kirchhoff

abemos, por lo estudiado en otros capítulos, que la suma de todas las caídas de tensión en cada rama de un circuito equivale a la tensión de la fuente. Esta es la base para la segunda Ley de Kirchhoff, que se enuncia así: "Las caídas de tensión en un circuito son iguales a la tensión total aplicada al circuito".

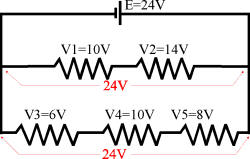
La suma de todas las caídas de tensión en cada rama es igual a la fuente (E)

El enunciado de esta ley, visualizado en el esquema superior, queda demostrado al sumar las caídas de tensión en cada rama:

V1 + V2 = 10 + 14 = 24 = E

V3 + V4 + V5 = 6 + 10 = 8 = 24 = E

Hallando una tensión desconocida

Siempre que entre dos uniones se conozcan todas las caídas de tensión menos una, ésta puede determinarse mediante la 2ª Ley de Kirchhoff.

En el esquema de ejemplo sabemos el valor de dos caídas de tensión (V1 y V3), y la caída total Vt entre las uniones A y B. Se trata de hallar la caída de tensión V2:

En base a la regla de la 2ª Ley de Kirchhoff, establecemos la igualdad:

Vt = V1 + V2 + V3

Y resolvemos la incógnita V2

V2 = Vt - V1 - V3 = 45 - 6 - 19 = 20 voltios

Hallando tensiones desconocidas en circuitos de varias ramas

En circuitos más complejos, de dos o más ramas, las caídas de tensión se hallan resolviendo primero las tensiones de cada rama, para después calcular la de sus resistencias interiores.

En el esquema del ejemplo, desconocemos V2 y V3. En primer lugar tenemos que hallar la tensión de las ramas paralelas entre los puntos A y B, empezando por la más sencilla, V2, pues conocemos los otros valores necesarios para resolverla (V1 y la tensión total Vt).

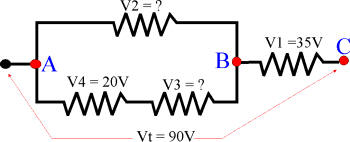
Así, establecemos la igualdad:

Vt = V1 + V2

Y hallamos la incógnita V2:

V2 = Vt - V1 = 90 - 35 = 55 voltios

Ahora, conociendo V2 ya podemos calcular V3:

V2 = V3 + V4

V3 = V2 - V4 = 55 - 20 = 35 voltios

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios