| Natureduca - Portal educativo de ciencia y cultura |

Física
ELECTRICIDAD
Circuitos de corriente continua - 7ª parte
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Circuitos serie
Introducción
 hora que ya hemos estudiado la Ley de Ohm,
podemos introducirnos en las tres disposiciones que puede adoptar un circuito de
corriente continua: serie, paralelo y serie paralelo, y realizar cálculos sobre
los tres parámetros básicos: voltaje, intensidad y resistencia.
hora que ya hemos estudiado la Ley de Ohm,
podemos introducirnos en las tres disposiciones que puede adoptar un circuito de
corriente continua: serie, paralelo y serie paralelo, y realizar cálculos sobre
los tres parámetros básicos: voltaje, intensidad y resistencia.
En algunos casos, es posible realizar cálculos de caídas de tensión en resistencias serie sin necesidad de aplicar estrictamente la ley de Ohm. Esto puede suceder cuando conocemos el voltaje de la fuente y el valor de las resistencias; para ello se aplica lo que se conoce como fórmula del divisor de tensión, que se explicará más abajo.
Características de los circuitos serie
Cuando hablamos de un circuito serie, estamos dando por hecho que agrupa al menos dos resistencias en serie, es decir, en línea. En esta disposición los valores totales de resistencia, corriente y voltaje presentan unas determinadas características que vamos a tratar a continuación, y que son fundamentos básicos para el estudio de cualquier otro circuito más complejo en el que intervengan componentes resistivos en serie:Resistencia
En un circuito serie las resistencias se suman, y ese valor es la oposición total que ofrece al paso de la corriente. Por ejemplo, si el circuito presenta dos resistencias en serie, una de 12 ohmios (R1) y la otra de 8 ohmios (R2), la resistencia total del circuito (Rt) será de 20 ohmios.

Corriente
La intensidad de corriente en un circuito serie es siempre la misma en cualquier parte de él. La corriente fluye por todos sus componentes, y si la medimos con un amperímetro observaremos que su valor no cambia, independientemente del punto elegido para medirla.Así, si en el circuito anterior hay una corriente de 0,5 amperios (más adelante aprenderemos a calcularla) esta corriente es la misma en R1, en R2 o en cualquier punto del cable a lo largo de todo el circuito. Si este circuito lo cortamos en algún punto, el flujo de corriente se interrumpirá.
Voltaje (caída de tensión)
Cuando un circuito serie está cerrado, la corriente que circula por cada resistencia provoca en ellas una caída de tensión (en voltios) proporcional a su valor (en ohmios), por tanto, el voltaje (caída de tensión) en las resistencias de un circuito serie, al contrario de lo que sucede con la corriente, varía según el valor de cada una de ellas.En cualquier caso, la suma total de los valores de tensión caídos en las resistencias es siempre igual al valor del voltaje de la fuente. Así, por ejemplo, si un circuito serie posee dos resistencias, en las cuales caen 6 y 4 voltios respectivamente, la suma de ambas caídas nos da el valor del voltaje de la fuente (E), en este caso E=6+4=10V.
Nota.- Más adelante, cuando estudiemos la ley de Kirchhoff, veremos que en un circuito puede existir más de una fuente de alimentación, y que cuando están conectadas en serie pueden sumarse u oponerse (según la orientación de sus polos), lo cual afecta sustancialmente al nivel de voltaje aplicado al circuito. Los valores de caída de tensión en las resistencia de un circuito serie pueden calcularse fácilmente aplicando la fórmula del divisor de tensión.Fórmula del divisor de tensión
En el circuito serie anterior si la fuente (E) fuese de 10 voltios, se distribuirá la tensión entre ambas resistencias proporcionalmente de acuerdo con su valor: 6 voltios para la resistencia de 12 ohmios, y 4 voltios para la resistencia de 8 ohmios.
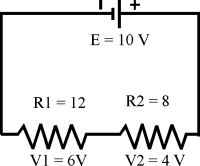
En nuestro caso, si deseamos calcular el valor de la caída de tensión (V) en R2 (V2), aplicaríamos la fórmula del divisor de tensión:

Esta fórmula puede aplicarse a cualquier circuito serie independientemente del número de resistencias que contenga, para ello sólo hay que sumar en el divisor tantos valores como resistencias agrupe el circuito, colocando siempre en el dividendo el valor de la resistencia cuya caída de tensión deseamos conocer.



