---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Circuitos paralelo (continuación)

Hallando la resistencia total o equivalente (continuación)

Circuito con resistencias desiguales

uando las resistencias conectadas en un circuito paralelo son desiguales, ya no podemos utilizar la sencilla fórmula explicada en la primera parte de este artículo, pues la oposición al flujo de la corriente es diferente en cada rama.

Por tanto, no tenemos un valor común a todas las resistencias para poder dividir ese valor entre el número de ellas. En su lugar, es necesario utilizar alguna fórmula en cuyo cálculo se combinen todos los diferentes valores.

Si es un circuito de dos resistencias desiguales:

Si se trata de un circuito con sólo dos resistencia desiguales aplicaremos la siguiente fórmula de productos entre sumas, es decir, multiplicando sus valores y dividiéndolos entre sus sumas.

Tomando como ejemplo dos resistencias en paralelo R1 y R2, de 60 y 40 ohmios respectivamente, nos daría una resistencia total equivalente de 24 ohmios:

Si es un circuito de tres o más resistencias desiguales:

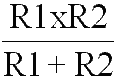
Cuando se trata de tres o más resistencias desiguales, se puede aplicar la misma fórmula de productos entre sumas, pero combinando las resistencias de dos en dos.

Tomando como ejemplo el circuito anterior, si le añadimos una resistencia más (R3) de 48 ohmios, hallamos primero la resistencia equivalente de R1 y R2, que llamamos Ra:

El resultado de Ra lo combinamos con R3 para obtener la resistencia total Rt.

De todas formas, para más de dos resistencias desiguales, es más práctico usar un método universal, el método "inverso", también llamado "recíproco".

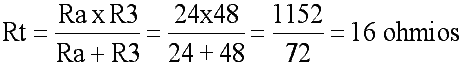
Método inverso

En este método es indiferente el número de resistencias desiguales que tenga el circuito. Si presenta muchas resistencias en paralelo, entonces es sin lugar a dudas el método más práctico. Su fórmula es:

Para simplificar los cálculos, tomando como ejemplo el mismo circuito anterior, resultaría:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios