/natureduca/fisica-electricidad-circuitos-de-corriente-continua-03

---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Ley de Ohm

na de las leyes más importantes de la electricidad fue enunciada en 1826 por el físico alemán George Ohm. Descubrió que en los circuitos eléctricos se daban unas sencillas relaciones entre el voltaje, la intensidad de la corriente y la resistencia.

Ohm observó dos interesantes parámetros:

1. Que sin variar la resistencia, la intensidad de corriente en un circuito aumentaba proporcionalmente al aumentar el voltaje.

2. Que sin variar el voltaje, la intensidad de corriente en un circuito disminuía cuando se aumentaba la resistencia.

Enunciado de la ley de Ohm

Las dos relaciones que Ohm observó constituyen en síntesis la ley que lleva su nombre, considerada como la más básica de los circuitos eléctricos. Esta ley se enuncia de la siguiente forma:

La intensidad que circula por un circuito varía en forma directamente proporcional a la variación del voltaje, y en forma inversamente proporcional a la variación de la resistencia.

De este enunciado se deduce, que cuando aumenta o disminuye el voltaje, aumenta o disminuye igualmente la intensidad de corriente en la misma proporción. Por su parte, cuando lo que aumenta o disminuye es la resistencia, entonces la intensidad de corriente también lo hace proporcionalmente, pero a la inversa.

Expresión matemática de la ley de Ohm

Matemáticamente, la ley de Ohm se expresa así:

Donde Ies la intensidad de corriente expresada en amperios (A),Ela fuerza electromotriz o voltaje expresada en voltios (V), y Rla resistencia expresada en ohmios (Ω). Así pues, amperios = voltios dividido entre ohmios.

Podemos demostrar esta ley haciendo un sencillo cálculo sobre un circuito serie:

En este circuito la fuente de alimentación E es de 10 voltios y la resistencia R de 10 ohmios. Aplicando la fórmula de la ley de Ohm, obtenemos que la intensidad I que circula por la resistencia es de 1 amperio:

Aplicando la fórmula básica de la Ley de Ohm:

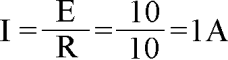
Si ahora cambiásemos la resistencia de 10 ohmios por otra del doble de valor (20 ohmios), quedaría demostrado cómo la corriente varía en forma inversamente proporcional a la resistencia. Así, aplicando la fórmula nos daría I=10/20=0,5 A. Por tanto para una resistencia de doble valor, manteniendo constante el valor del voltaje, la corriente se ha reducido a la mitad, es decir, ha variado proporcionalmente pero a la inversa.

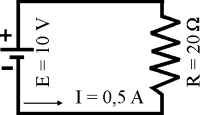
Si aumentamos la resistencia al doble manteniendo constante el voltaje, la intensidad varía proporcionalmente pero a la inversa (decrece)

De la misma manera, si cambiásemos la fuente por otra de doble voltaje (20 voltios), quedaría demostrado como la corriente varía en forma directamente proporcional a la tensión. Así, aplicando la fórmula nos daría I=20/10=2 A. Por tanto, para un voltaje de doble valor, manteniendo constante la resistencia, la corriente también se ha incrementado el doble, es decir, ha variado proporcionalmente de forma directa.

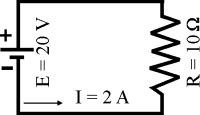
Si aumentamos la fuente al doble de tensión manteniendo constante la resistencia, la intensidad varía proporcionalmente de forma directa (crece)

Conociendo la intensidad y la resistencia...

La fórmula básica de la ley de Ohm se puede despejar para obtener una magnitud conociendo las otras dos. Por ejemplo, sabiendo el valor de la intensidad (I) y de la resistencia (R) podemos obtener la magnitud del voltaje de la fuente (E).

En nuestro primer circuito de ejemplo, siendo I=1A y R=10 ohmios, resulta:

E = IR = 1 x 10 = 10 V

Conociendo el voltaje y la intensidad...

Igualmente, sabiendo el valor del voltaje (E) y de la intensidad de corriente (I) se puede obtener la magnitud de la resistencia (R). Considerando el mismo circuito anterior, resulta:

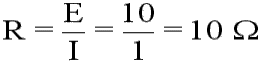
Observaciones:

En la práctica, cuando se expresan las fórmulas de las leyes eléctricas no se utilizan los signos de multiplicación. Así, la fórmula E = I x R, se expresa como: E=IR.

Igualmente, las cantidades que se utilicen deben corresponder siempre a las unidades básicas de intensidad, voltaje y resistencia. Si esas cantidades estuvieran expresadas en unidades mayores o menores, por ejemplo miliamperios, kilovoltios o megohms,  hay que convertirlas primero a amperios, voltios u ohmios, respectivamente.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios