/natureduca/fisica-electricidad-circuitos-de-corriente-continua-17

---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Circuitos serie-paralelo (continuación)

n ocasiones desconocemos el valor de las resistencias de un circuito serie-paralelo, o sólo nos interesa resolver una parte del mismo. Para ello, existen las dos leyes de Kirchhoff, una relativa a corrientes, y otra a tensiones.

A lo largo de lo estudiado en los capítulos anteriores, ya hemos conocido y utilizado, sin nombrarlos, estas dos reglas, cuando nos referíamos a flujos de corriente y caídas de tensión en los diferentes tipos de circuito. Ahora, vamos a emplear las reglas para hallar cantidades desconocidas en circuitos serie-paralelo.

Primera ley de Kirchhoff

Ya sabemos que la corriente en un circuito sale de un polo de la fuente, recorre los componentes y vuelve a la fuente por el otro polo, y que la misma corriente que entra en el circuito es la misma que sale de él. La primera Ley de Kirchhoff se basa precisamente en este hecho. Dice: "La corriente que entra en una unión de un circuito es la misma que abandona esa unión".

Ejemplo A

Consideremos una parte de un circuito compuesta por una resistencia (R1), con un punto de unión a dos ramas con sendas resistencias (R2 y R3). Conocemos la dirección e intensidad de la corriente en R2 (I2) y R3 (I3). Se trata de hallar la intensidad desconocida en R1 (I1):

Sabemos por la 1ª Ley de Kirchhoff, que la corriente que entra en un punto o unión es la misma que sale de él. En el ejemplo, la flecha indica que la corriente va hacia la unión y sale dividida en dos ramas. Por tanto, la suma de las dos corrientes que salen de la unión tiene que ser, forzosamente, igual a la corriente que entra en la unión. Así, resulta:

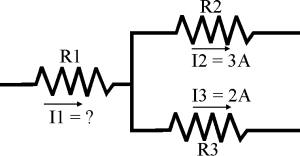
I1 = I2 + I3 = 3 + 2 = 5 amperios

Ejemplo B

Consideremos un circuito con dos ramas de entrada y otras dos de salida de un mismo punto común. Cada una de ellas presenta una resistencia (R1, R2, R3 y R4), y sabemos cuáles son sus intensidades de corriente, excepto la que circula por R1 (I1).

En el ejemplo "A" anterior había una sola rama de entrada y dos ramas de salida. En este otro ejemplo da igual de cuántas ramas se trate, la suma de las intensidades de corriente que salen de una unión es siempre la intensidad total que entra en ella, así que la suma de I3 e I4 (salida) tiene que ser igual a la suma de I1 e I2 (entrada). Por tanto, podemos plantear la siguiente igualdad:

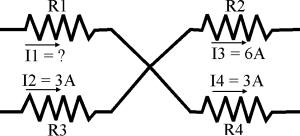
I1 + I2 = I3 + I4

I1 + 3 = 6 + 3

I1 + 3 = 9

En esta igualdad nos ha quedado una  incógnita (I1). Pasando el término que está sumando al otro extremo de la ecuación con signo opuesto, obtendremos finalmente el valor de I1, que es la corriente que nos falta.

I1 = 9 - 3  = 6 amperios

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios