---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Aplicando la ley de Ohm a circuitos paralelo

on la Ley de Ohm podemos hallar valores desconocidos de corriente, voltaje, resistencia o potencia en un circuito, si disponemos de al menos dos valores conocidos.

A continuación resolveremos algunos problemas aplicando esta ley, así como los métodos ya estudiados anteriormente para obtener los valores equivalentes de resistencia en circuitos paralelo.

Problema 1

Consideremos un circuito paralelo con tres resistencias, R1, R2 y R3, cuyos valores se desconoce. Sabemos que la tensión es de 45 voltios, y en cuanto a las corrientes conocemos todas (incluida la corriente total) excepto la que circula por R3 (I3).

Se trata de hallar todos los valores restantes, y la potencia total y parcial de cada resistencia.

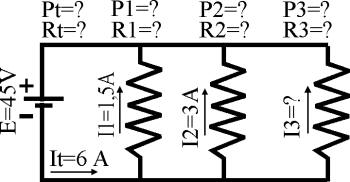
Antes de nada, lo procedente es hacer un cuadro con todos los valores disponibles, e ir cubriéndolo con todos los demás que vayamos obteniendo. Se conoce el voltaje de la fuente (E), que son 45 voltios, pero como en un circuito paralelo la tensión es la misma en todas las ramas, ya sabemos también la caída de tensión en cada una de las resistencias, por lo cual ya podemos anotarlas en nuestro cuadro.

De R1 y R2 conocemos su voltaje e intensidad de corriente, por tanto ya podemos calcular su resistencia:

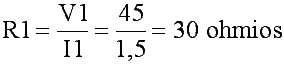
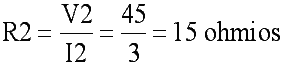
Para hallar R3, tenemos que calcular primero el valor de la corriente que circula por ella (I3). Sabemos que la intensidad total en un circuito paralelo es la suma de las intensidades de cada rama, y conocemos la intensidad total It (6 amperios), y la intensidad de R1 (1,5 amperios) y R2 (3 amperios), por tanto la corriente que circula por R3 tiene que ser forzosamente la resultante de restar a la intensidad total la suma de I1 e I2.

I3 = It - (I1+I2) = 6 - (1,5 + 3) = 1,5 amperios

Ahora, conociendo I3, podemos hallar el valor de R3:

Para hallar la resistencia total podemos utilizar el método inverso:

O también el método de productos entre sumas, combinado las resistencias de dos en dos, primero R1 y R2 (que llamaremos Ra) y después Ra y R3.

Con los valores obtenidos, calcular la potencia resulta sumamente sencillo, pues ya conocemos todos los voltajes, corrientes y resistencias. Para ello podríamos utilizar cualquiera de las tres fórmulas:

1. P = E I

2. P = E2 / R

3. P = I2 R

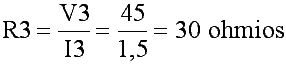
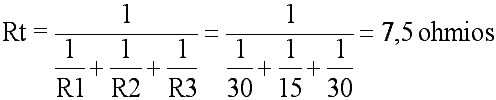
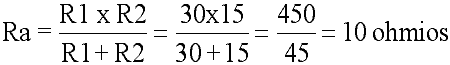
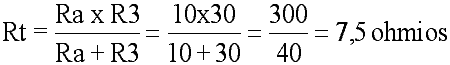
Evidentemente, la fórmula más sencilla de aplicar es P=E I. Calcularemos la potencia en cada una de las resistencias (P1, P2 y P3) y la potencia total de todas ellas (Pt):

P1 = V1 x I1 = 45 x 1,5 = 67,5 W

P2 = V2 x I2 = 45 x 3 = 135 W

P3 = V3 x I3 = 45 x 1,5 = 67,5 W

Pt = E x It = 45 x 6 = 270 W

Hemos hallado la potencia total tomando como valores el voltaje de la fuente y la intensidad total, pero, si hemos realizado correctamente todos los demás cálculos, podemos hacer la prueba de sumar todas las potencias individuales, y nos tendría que dar exactamente el mismo valor:

Pt = P1 + P2 + P3 = 67,5 + 135 + 67,5 = 270 W

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios