/natureduca/tecnologia-tecnica-informatica-representacion-de-la-informacion-11

---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

El sistema de numeración hexadecimal (continuación)

Conversión directa de hexadecimal a binario y viceversa

na de las grandes ventajas del sistema hexadecimal es la posibilidad que tiene de permitir el paso directo de un número hexadecimal a binario.

En efecto, se puede realizar la conversión directa entre los sistemas de numeración binario y hexadecimal, sin más que tener en cuenta la expresión de los dígitos de la base hexadecimal en la base binaria.

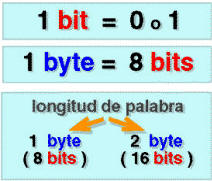
La relación entre el sistema binario y el hexadecimal es ideal por su conversión directa de uno a otro, y por la posibilidad de aprovechar los dieciséis símbolos distintos que posee cuando combina cuatro cifras binarias.

Una de las razones que justifican la existencia y el amplio uso que se hace del sistema de numeración hexadecimal es la que se expone a continuación. Si consideramos un número binario de una sola cifra se podrán representar como máximo dos estados: el 0 y el 1. Por tanto, no podríamos representar las ocho cifras restantes del sistema de numeración decimal (del 2 al 9).

Con un número binario constituido por dos cifras ya se pueden obtener representaciones de cuatro cifras decimales (del 0 al 3), faltando todavía la posibilidad de representar las seis cifras decimales restantes (del 4 al 9).

Con un número binario de tres cifras, se pueden representar hasta ocho cifras decimales ya que 2³ = 8; en definitiva, en sistema binario un número de n cifras puede representar 2ⁿ estados o cifras decimales.

Por tanto, un sistema de numeración binario de sólo tres cifras no es suficiente para representar todas las cifras decimales ya que 2³ = 8, por tanto se necesitan al menos cuatro cifras binarias. Pero resulta que 2⁴ = 16 con lo que se usarían las diez primeras combinaciones de cuatro cifras binarias para representar las diez cifras decimales, pero se desperdician seis combinaciones que no tendrían significado en decimal.

Sin embargo, si se usa un sistema de numeración hexadecimal que está compuesto por dieciséis símbolos distintos, se consigue aprovechar todas las combinaciones posibles de cuatro cifras binarias sin desperdiciar ninguna combinación.

Veamos algún ejemplo de conversión.

Problema n 1

Convertir el número binario 1111011100001 a hexadecimal. En primer lugar se agrupan los dígitos, empezando por la derecha de cuatro en cuatro, completando el último grupo de la izquierda con ceros si es necesario; después se averigua para cada grupo de cuatro cifras binarias su correspondiente cifra hexadecimal (ver tabla de equivalencias entre sistemas) y obtendremos la expresión hexadecimal directamente:

por tanto, el número en hexadecimal sería:

1EE1₍₁₆

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios