339 usuarios conectados
/natureduca/tecnologia-tecnica-informatica-representacion-de-la-informacion-08
Tecnología
TÉCNICA INFORMÁTICA
Representación de la información - 8ª parte
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
El sistema de numeración decimal
l que empleamos normalmente es el sistema decimal o de
base diez. Fue ideado por los indios en el siglo VI a. de J.C. y traído a
Europa por los árabes en la Edad Media y está basado en el número 10 por ser
éste el número de dedos de las manos, y ser un medio muy natural para
contar.
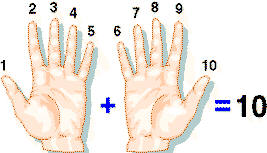
El ser humano encontró en
los diez dedos de las dos manos los elementos más próximos y naturales
para contar. El número 10 se estableció como base numérica, en función
de la cual se fundamentaron todos los demás parámetros de este sistema:
unidad (1), decena (10), centena (100), millar (1000), etc.
Consta de diez símbolos diferentes: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9, que debidamente agrupados pueden representar cualquier número.
El valor de cada símbolo es igual a su valor absoluto multiplicado por las sucesivas potencias de 10 (siempre de derecha a izquierda).Así, por ejemplo, el número 3.125 equivale a:
(3 x 103) + (1 x 102) + (2 x 101) + (5 x 100)
o lo que es igual:(3 x 1000) + (1 x 100) + (2 x 10) + (5 x 1)
El sistema de numeración binario
Tiene por base 2, es decir, sólo utiliza dos símbolos: 0 y 1. Sus principales ventajas son la sencillez de su aritmética y la facilidad de encontrar sistemas físicos que puedan tener dos estados.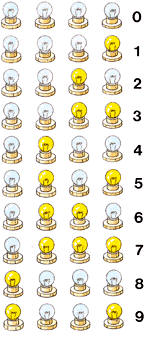
El
código BCD permite pasar a código binario cualquier número u
operación en código decimal. Dado que los aparatos electrónicos
empleados en informática únicamente entienden el código binario, el
sistema BCD es fundamental para especificar órdenes y procesos en
código máquina
El principal inconveniente de este sistema es el número de dígitos necesarios para representar cualquier cantidad, pero en contrapartida un simple circuito abierto o cerrado (abierto = 0 ó desactivado, cerrado = 1 ó activado) será capaz de representar los dos estados de este sistema.
© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación -
www.asocae.org - RNA 592727 - CIF.: G70195805 ¦
Quiénes somos ¦
Contacto ¦
Bibliografía ¦
Política de privacidad ¦
Esta web NO utiliza cookies, ni guarda datos personales de los usuarios