| Natureduca - Portal educativo de ciencia y cultura |

Tecnología
TÉCNICA INFORMÁTICA
Electrónica digital - 8ª parte
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Álgebra de Boole
Definición
 l álgebra de Boole es un conjunto de elementos relacionados por
dos operaciones binarias a las que notaremos con los signos + y - que verifican
los siguientes postulados:
l álgebra de Boole es un conjunto de elementos relacionados por
dos operaciones binarias a las que notaremos con los signos + y - que verifican
los siguientes postulados:
a + b = b + a y a . b = b . a
2. Las operaciones + y . tienen elementos neutros, a los que denominaremos 0 y 1 respectivamente. Es decir, si a es un elemento del álgebra:a + 0 = a
a . 1 = a
3. Cada operación es distributiva respecto de la otra. Es decir, si a, b, c, son elementos del álgebra:a . (b + c) = a . b + a . c
a + (b . c) = (a + b) . (a + c)
4. Para cada elemento a del álgebra existe otro elemento, al quedenominaremos
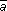 , tal que se
verifica:
, tal que se
verifica:
a +
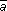 = 1
= 1
a .
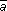 = 0
= 0
A nosotros nos interesarán los denominados álgebras de Boole binarios, que constan de elementos que toman sólo dos valores: 0 ó 1, cuyas operaciones + y - se definen de la forma:
Para la operación +, o suma binaria:0 + 0 = 0
0 + 1 = 1 + 0 = 1
1 + 1 = 1
Para la operación ., o multiplicación binaria:0 . 0 = 0
0 . 1 = 1 . 0 = 0
1 . 1 = 1
Y además:
![]() = 1
= 1
![]() = 0
= 0
O expresadas tabularmente en forma de tablas de verdad:
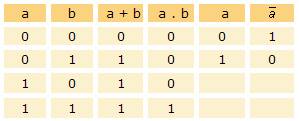
Ejemplos de álgebras de Boole binarias son las que se tratan a continuación en las páginas siguientes.



