---

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Simplificación de un circuito con puertas lógicas (continuación)

or tanto, por lo dicho en la página anterior, una vez que se disponga de la expresión algebraica que determina la función lógica que queremos realizar, es preciso simplificarla lo más posible.

Vamos a ver mediante un sencillo ejemplo de cómo se simplifican las funciones lógicas.

Sea la función lógica F dada por la expresión siguiente:

El circuito que responde a esta expresión es el representado en el esquema adjunto.

El término A, según una propiedad del álgebra de Boole binario, es igual a 1, por lo que la expresión de F será igual a:

Aplicando la propiedad distributiva al término B, tendríamos:

y la expresión de F sería:

Pero según hemos visto antes, Z + = 1, por lo que quedaría:

Aplicando la propiedad distributiva al término C, en sentido contrario al empleado la vez anterior, tendremos la siguiente expresión para F.

Pero sabemos por las propiedades definidas para el álgebra de Boole que X . X = X y que X . X = 0, por tanto:

por tanto, el circuito quedaría simplificado al de la figura adjunta, y teniendo en cuenta que los inversores (puertas NOT) no son necesarios por no ser preciso efectuar ninguna inversión, el circuito final que realizaría exactamente las mismas funciones que el del circuito de partida, podría ser representado mediante el esquema adjunto.

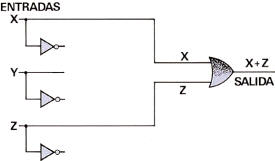
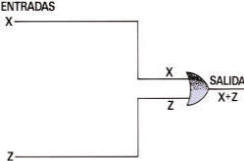
A la izquierda, un circuito lógico de partida; a la derecha, el circuito equivalente

Sobre la importancia de la simplificación de funciones lógicas para la fabricación de circuitos digitales, no es preciso más que reparar en que mientras que para la realización del circuito de partida eran necesarias 12 puertas lógicas (3 puertas NOT, 5 puertas AND y 4 puertas OR), el circuito equivalente (figura adjunta) está constituido por una simple puerta OR.

1 2 3 4 5 6 7 8 9 10 11 12 13 14

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios