| Natureduca - Portal educativo de ciencia y cultura |

Química
ESPECTROS, ÁTOMOS Y NÚCLEOS
El núcleo atómico - 3ª parte
La desintegración radiactiva (continuación)
 a desintegración radiactiva de una especie nuclear dada lleva
consigo la disminución del número de núcleos de esa especie presente en la
muestra.
a desintegración radiactiva de una especie nuclear dada lleva
consigo la disminución del número de núcleos de esa especie presente en la
muestra.
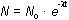
(16.15)
El periodo de semidesintegración T es otra magnitud que
caracteriza el comportamiento radiactivo de un isótopo. Se define como el tiempo
necesario para que el número de núcleos radiactivos de una muestra dada se
reduzca a la mitad. Su relación con la constante de desintegración
![]() viene dada
por la ecuación T = 0,693/
viene dada
por la ecuación T = 0,693/![]() y su valor puede variar desde una fracción de
segundo hasta cientos de años en función del núcleo considerado. La vida media
y su valor puede variar desde una fracción de
segundo hasta cientos de años en función del núcleo considerado. La vida media
 es el valor promedio de la vida de los núcleos de una
especie radiactiva dada. Coincide con el inverso de la constante de
desintegración
es el valor promedio de la vida de los núcleos de una
especie radiactiva dada. Coincide con el inverso de la constante de
desintegración  = 1
= 1![]() /
/
Los isótopos radiactivos tienen un elevado número de aplicaciones en la industria, en la investigación física y biológica y en la medicina. Así se recurre al análisis de un isótopo del carbono C14 para determinar edades de restos fósiles; se utilizan isótopos radiactivos en biología como elementos trazadores, que incorporados a moléculas de interés, permiten seguir su rastro en un organismo vivo. Su empleo en radioterapia hace posible el tratamiento y curación de diferentes tipos de enfermedades cancerosas.
Aplicación de los conceptos fundamentales de la desintegración
El periodo de semidesintegración T del 92U238 para la desintegración es 4,5 · 109 años. Calcular: a) La constante de desintegracióna) La constante de desintegración
![]() está relacionada con el
periodo T por la ecuación
está relacionada con el
periodo T por la ecuación
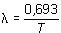
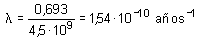
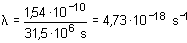
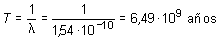
Por tanto:
A = N



