---

1 2 3 4 5 6 7

Movimientos en vertical (continuación)

na situación más complicada, pero también más frecuente, es aquella en la que el cuerpo se desplaza en el seno de un medio resistente, como el aire. En tal caso el rozamiento da lugar a una fuerza Froz que se opone al movimiento. Si la velocidad no es muy grande puede considerarse, en una primera aproximación, que dicha fuerza es constante.

El estudio dinámico del movimiento de caída supondrá ahora determinar la resultante de las fuerzas que actúan, que en este caso son el peso Phacia abajo y la Froz hacia arriba. Se trata de fuerzas con la misma dirección y sentidos opuestos cuya resultante estará dirigida hacia abajo, es decir, según el sentido del movimiento, y cuya magnitud será la diferencia entre ambas. La segunda ley de Newton da lugar, en este caso, a la ecuación:

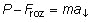
es decir, la aceleración de caída a resulta ser

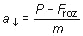
De acuerdo con (2.5), P = mg, luego sustituyendo en la ecuación anterior, se tendrá:

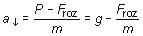
(2.6)

La aceleración de caída es constante si Froz se puede considerar como constante, pero el movimiento gana velocidad más lentamente que en el caso anterior. De nuevo y por ser a¯ constante pueden aplicarse todas las fórmulas cinemáticas del movimiento rectilíneo uniformemente acelerado. A partir de las fuerzas, pueden entonces determinarse las características del movimiento.

Si el cuerpo no cae, sino que es lanzado verticalmente hacia arriba con una velocidad inicial vo el análisis dinámico es análogo al anterior. Si se toma como sentido de referencia el del movimiento, la utilización de las tres primeras reglas de aplicación de la segunda ley dará lugar a la siguiente ecuación:

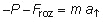
El signo negativo afecta ahora a ambas fuerzas pues en este caso el peso, al igual que la fuerza de rozamiento, se opone al movimiento. Despejando la aceleración de subida a de la anterior ecuación resulta:

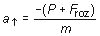
es decir:

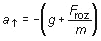
(2.7)

La aceleración del movimiento resultante es ahora negativa. Se trata de un movimiento decelerado en el que el móvil termina por perder completamente la velocidad inicial vo. El hecho de que vo no aparezca de forma explícita en la ecuación (2.7) no significa que no haya de tomarse en consideración; vo no es ni una fuerza ni una aceleración, por eso no figura en la segunda ley; sin embargo, la determinación a partir del valor de a­ de otras variables cinemáticas como altura máxima que alcanza el cuerpo o tiempo que tarda en conseguirla requerirán su utilización.

En el movimiento de caída libre se consideran despreciables, o en su caso inexistentes, las fuerzas de rozamiento del cuerpo con el aire u otro medio resistente. La única fuerza que actúa es entonces, la fuerza del peso

1 2 3 4 5 6 7

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios