Con la teoría heliocéntrica La Tierra pasó a ser un simple planeta más del Sistema Solar, perdiendo su posición de centro del Universo que le otorgaba la teoría geocéntrica
Primeras teorías cosmológicas
Del siglo IV a.C. datan las primeras teorías cosmológicas, centradas en los pueblos mesopotámicos, los cuales consideraban que la Tierra era el centro del Universo, y que eran los demás cuerpos celestes los que giraban alrededor de ella. Algunos clásicos como Aristóteles, defendían esta teoría.
El filósofo, matemático y astrónomo Anaximandro de Mileto, discípulo y amigo de Tales de Mileto, es mencionado como fundador de la cosmología. Su concepción del Universo se basaba en un número de cilindros concéntricos, de los cuales el más exterior era el Sol, la Luna el del medio, y las estrellas contenidas en el del interior. La Tierra se encontraba dentro de estos cilindros. Defendía una teoría del origen del Universo en la cual se postulaba que era resultado de la separación de opuestos desde la materia primaria; el calor se habría movido hacia fuera, separándose de lo frío, y más tarde lo habría hecho lo seco de lo húmedo. Sostenía además, que todas las cosas vuelven con el tiempo al elemento que las originó.
Otro clásico del siglo II, Claudio Tolomeo, intentó tomar en consideración un modelo heliocéntrico, pero lo desechó basándose en la física de Aristóteles, en la cual no tenía cabida una rotación de la Tierra sin que ésta resultase violenta y convulsa. En su lugar adoptó el modelo de que las estrellas se movían en la noche porque se encontraban encerradas en unas esferas cristalinas giratorias, perfectas y transparentes. Tiempo después el modelo geocéntrico de Tolomeo seguía firmemente apoyado por la Iglesia, de tal forma que ayudó a frenar considerablemente el progreso de la astronomía durante los siguientes mil años.
A pesar de que el astrónomo griego Aristarco de Samos sostuvo también en el 270 a.C. que la Tierra giraba alrededor del Sol, su teoría quedó nublada por la autoridad del propio Aristóteles, la cual no fue rebatida hasta mucho siglos después. De hecho, el sistema geocéntrico imperó totalmente hasta finales de la Edad Media, a pesar de algunos intentos por cambiarlo por el heliocéntrico.
La audaz hipótesis de Copérnico
En el año 1543, la explicación del movimiento de los planetas era para el clérigo y astrónomo polaco Nicolás Copérnico, mucho más fácil si se situaba al Sol como centro del Universo. En la hipótesis de Copérnico los planetas, incluido la Tierra, trazaban sus órbitas alrededor del Sol. Esta teoría se fue imponiendo sobre las demás, pero muy lentamente.

Nicolás Copérnico
Gran parte de la fama de Copérnico se debe a la obra Revoluciones de los cuerpos celestes (1543), donde realiza un análisis crítico de la teoría de Tolomeo sobre un Universo geocéntrico. La proposición de que fuera el Sol y no la Tierra el centro del Universo, fue el rasgo más audaz de Copérnico, quedando la Tierra degradada a la categoría de un simple planeta más. Su teoría molestó a muchas personas y fue contestada duramente por la Iglesia, que incluyó su obra en la lista de libros prohibidos en 1616, donde permaneció hasta 1835.
Las pruebas de Galileo Galilei
El sistema heliocéntrico de Copérnico no obtuvo suficiente atención, hasta que Galileo Galilei descubrió pruebas tangibles para defender esta teoría.

Galileo Galilei
En 1609, Galileo fue uno de los primeros en observar los planetas a través de un telescopio; pudo comprobar como algunos planetas giraban alrededor del Sol y no de la Tierra. Galileo comenzó entonces a escribir y publicar en favor de la teoría de Copérnico, convirtiéndose en un fiel defensor de ésta, pero el intento de difundirla le llevó ante un tribunal de la inquisición, el cual le obligó a renegar de sus creencias y escritos bajo acusación grave de herejía. A pesar de ello, la teoría de Copérnico no pudo ser eliminada.
La quintaesencia y la armonía del círculo
Para comprender las dificultades de resolución de los problemas orbitales que tuvieron los observadores y teóricos que siguieron a Galileo (principalmente Kepler), es necesario comprender los misticismos sobre la matemática y geometría arrastrados desde la época de Pitágoras.
Pitágoras, en el siglo VI a.C., fue el primero en utilizar la palabra Cosmos, es decir, el concepto de Universo ordenado y armonioso. Sus discípulos relacionaban la certeza de la demostración matemática con la perfección del Universo. Muchos de ellos eran místicos convencidos. La realidad de su imperfecto y desordenado mundo cotidiano, chocaba frontalmente con aquel Cosmos en el cual los lados de triángulos rectángulos obedecían a la perfección simples relaciones matemáticas; habían penetrado en la realidad perfecta del reino de los dioses.

Pitágoras
Los pitagóricos identificaban la constitución del mundo en cuatro elementos: tierra, fuego, aire y agua. Por su parte, por alguna razón éstos fueron identificados con cuatro sólidos regulares: cubo (6 cuadrados), tetraedro (4 triángulos equiláteros), octaedro (8 pentágonos) e icosaedro (20 triángulos equiláteros). Sin embargo, aunque existen infinitos polígonos regulares, sólo hay cinco sólidos regulares, el quinto es el dodecaedro, que tiene por lados a doce pentágonos. Por razones místicas pensaron entonces que el dodecaedro sólo podía relacionarse con el Cosmos y la sustancia de los cuerpos celestiales, de ahí la palabra quintaesencia dada a esta correspondencia físico-mística. Igualmente, los números enteros semejaban la racionalidad de las cosas, y creían que de ellos podían derivarse todas las incógnitas.
Por el carácter doctrinal de estas enseñanzas, la existencia del dodecaedro fue ocultada al pueblo llano, y sólo se manejaba dentro del ámbito de la escuela pitagórica. Por la misma razón, se ocultó un descubrimiento que rompía con la tan alabada armonía geométrica y matemática de los números enteros, y que produjo una verdadera crisis en esta doctrina. Simplemente, aplicando el teorema de Pitágoras, se comprobó que la raíz cuadrada de 2 (razón entre diagonal y lado de un cuadrado) no era racional, es decir, no podía expresarse con dos números enteros, de ahí la palabra irracional, significado de que un número no puede expresarse como una razón. Fue entonces cuando la concepción del mundo que mantenían Pitágoras y sus seguidores sintió una amenaza, la creencia de que podía desmoronarse ante el indicio de que esa concepción cosmológica careciera de sentido. De nuevo, el conocimiento de la raíz cuadrada de 2 fue ocultado como ya se hiciera con el dodecaedro, y reservado sólo como un conocimiento sagrado. Un discípulo de Pitágoras llamado Hispaso publicó el secreto del dodecaedro, pero su libro no trascendió y él pereció en un naufragio, en lo que fue considerado un castigo justo por los demás fieles de Pitágoras.
Pero uno de los elementos que favorecieron el lento avance en el desvelo de las leyes que rigen el Cosmos y el movimiento de los cuerpos planetarios, fue el concepto místico que tenían los pitagóricos del círculo y la esfera. Para ellos, la esfera era perfecta, pues el centro se encontraba a la misma distancia de cualquier punto de la superficie. El mismo concepto se tenía del círculo. Por esta razón, no se deducía otra forma de movimiento de los planetas que no fuera en forma circular, cualquier otra sugerencia indicaría un movimiento defectuoso e impropio, y mucho menos que la velocidad de la órbita fuese más o menos lenta a lo largo de ella.
Johanes Kepler no se libró de estas creencias (véase el siguiente apartado), que perduraron vigentes durante muchos siglos, y que desviaron la atención de los astrónomos teóricos de la auténtica realidad.
Las valiosas observaciones de Tycho Brahe y los revolucionarios descubrimientos de Johanes Kepler
as observaciones que realizó el astrónomo danés Tycho Brahe hasta finales del siglo XVI, en el observatorio que construyó en la isla de Hveen, en el Báltico, fueron muy valiosas para su ayudante, el matemático y astrónomo alemán Johanes Kepler. Sin embargo, Tycho Brahe no facilitó en principio sus observaciones a Kepler, a pesar de la impaciencia de éste por conocerlas, ni permitió compartir experiencias; más aún, las peleas y reconciliaciones eran continuas.
Tycho era un hombre muy rico, bastante extravagante, con una nariz de oro que suplía la original perdida en un duelo estudiantil; siempre estaba rodeado de un gran séquito de ayudantes, parientes y personas aduladoras. Kepler, por su parte, necesitaba las observaciones de Tycho para progresar en la síntesis de un sistema coherente del mundo. Mientras que Tycho era un genio en la observación estelar de la época, Kepler era el mayor teórico. Como el propio Kepler escribió “…Tycho posee las mejores observaciones… También tiene colaboradores. Solamente carece del arquitecto que haría uso de todo este material.”

Tycho Brahe
En el lecho de muerte Tycho legó todas sus observaciones a Kepler. Éste analizó y estudió después sus tablas astronómicas de gran exactitud, permitiéndole obtener un esquema numérico que explicase el sistema planetario. Además, Kepler tuvo ocasión de observar una de las pocas explosiones de una estrella supernova ocurridas en nuestra galaxia; siguió su evolución desde octubre de 1604 hasta comienzos de 1606, en que ya no era visible a simple vista, dándole argumentos en su tiempo para evidenciar la mutabilidad de las estrellas.

Johanes Kepler
Kepler perfeccionó el modelo de Copérnico adoptando su teoría, es decir, considerando que la Tierra giraba alrededor de su eje a la vez que se desplazaba en una órbita alrededor del Sol. Sin embargo, se resistió a desechar que los planetas se movían siguiendo caminos circulares, pues esto se daba por sentado; el círculo era considerado una figura geométrica perfecta, y en un sentido místico así eran considerados los movimientos de los planetas (véase el apartado anterior sobre la quintaesencia y la armonía del círculo). Kepler no fue ajeno a la idea pitagórica de un mundo perfecto y místico, resultando ésta parte principal de su formación más temprana, no siéndole nada difícil aceptar el concepto de que en el Universo reinaban proporciones armónicas matemáticas. Por tanto, el movimiento circular de los planetas era para él el único admisible de principio a fin.
Incluso Copérnico y los anteriores Galileo y Tycho, creían firmemente en las órbitas circulares y uniformes de los planetas, y cualquier otra cosa era impensable. Por ello, Kepler intentó una tras otra durante varios años confirmar las órbitas circulares, pero los resultados no encajaban. Cuando Kepler abandonó derrotado el estudio de la órbita circular para experimentar sobre otra en forma de elipse, se dio cuenta de cuanto tiempo había perdido por su fascinación hacia el círculo, ahora todo encajaba a la perfección.
Tras 16 años de intenso trabajo formuló las tres leyes que llevan su nombre, y que describen el movimiento de los planetas, en lo que pueden ser considerados unos descubrimientos astronómicos revolucionarios para su época. No obstante, Kepler se vio obligado a ir descartando progresivamente las clásicas teorías geocéntricas que imperaron durante muchos siglos. A partir de este momento las órbitas de los planetas se consideraron elípticas, quedando firmemente establecida la teoría heliocéntrica.
Leyes de Kepler
Primera: Cada planeta en su movimiento describe una elipse, en uno de cuyos focos se encuentra el Sol
Observando Marte, Kepler comprobó que giraba alrededor del Sol siguiendo una elipse en lugar de un circunferencia.
La circunstancia de que fuera Marte y no otro planeta del Sistema Solar el observado, fue una fortuita coincidencia, pues Marte posee la órbita más elíptica en comparación con los demás planetas. Si hubiera estudiado, por ejemplo a Venus, Kepler nunca habría descubierto las verdaderas órbitas de los planetas.
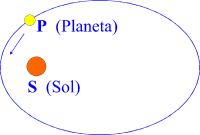
Primera ley de Kepler: Un planeta (P) se mueve siguiendo una elipse con el Sol (S) en uno de sus focos
En las órbitas elípticas el Sol nunca está en el centro, sino que se encuentra desplazado en un foco de la elipse. Se puede decir que los planetas “caen hacia el Sol”, pues cuando uno de ellos que siga una órbita elíptica se encuentra próximo al Sol, se acelera. Por el contrario, va más lento cuando está en el punto más alejado de él.
Segunda: Las áreas barridas por el radio vector que une un planeta con el Sol, son iguales en tiempos iguales
Si un cuerpo realiza un movimiento circular uniforme, recorrerá en tiempos iguales un ángulo igual o una fracción igual del arco del círculo.
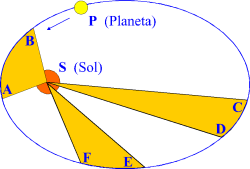
Segunda ley de Kepler: Un planeta barre áreas iguales en tiempos iguales. El tiempo que necesita el planeta P para ir de B a A es el mismo que necesita para ir de Fa E y de D a C; las áreas sombreadas que barre BSA, FSE y DSC son iguales
En una circunferencia se precisa doble tiempo para recorrer dos terceras partes, que para recorrer solamente un tercio de ella. Sin embargo, Kepler descubrió que en una órbita elíptica no se cumplía esta característica. Así, por ejemplo, un planeta al moverse a lo largo de la elipse en su órbita alrededor del Sol, cuando se encuentra próximo a él, traza en un periodo de tiempo dado un arco grande, sin embargo el área de ese arco es pequeña precisamente por su proximidad al Sol. Al contrario, cuando el planeta se encuentra alejado del Sol, para el mismo periodo de tiempo cubre un arco mucho más pequeño, pero que corresponde a un área mayor por encontrarse el Sol más distante. Pues bien, Kepler descubrió que tanto el área mayor (cuando está lejos del Sol), como la menor (cuando está más próximo) eran exactamente iguales, independientemente de lo elíptica que fuera la órbita.
Tercera: Los cuadrados de los períodos de revolución, es decir, los tiempos empleados por cada planeta en describir una órbita completa, son proporcionales a los cubos de los semiejes mayores de las órbitas, o sea a los cubos de sus distancias medias al Sol
Años después de que Kepler enunciara sus dos primeras leyes, descubrió su tercera y última ley o ley armónica. Ésta relaciona entre sí el tamaño de la órbita de un planeta y el periodo necesario para dar una vuelta alrededor del Sol.
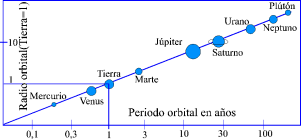
La tercera ley de Kepler, o ley armónica, relaciona de modo preciso el tamaño de la órbita de un planeta y el periodo que necesita para describir una órbita alrededor del Sol.
Cuanto más distante está el planeta, más lento es su movimiento, pero de acuerdo con una ley matemática precisa: P2=a3; donde P es el periodo de rotación alrededor del Sol medido en años, y a es la distancia que existe entre el planeta y el Sol medido en unidades astronómicas (u.a.). Así, por ejemplo, Júpiter está a 5 unidades astronómicas, por tanto: a3=5×5×5=125, dando como resultado un periodo de rotación P=11 aproximadamente, lo que significa que Júpiter precisa 11 años para dar una vuelta alrededor del Sol.





