| Natureduca - Portal educativo de ciencia y cultura |

Química
ESPECTROS, ÁTOMOS Y NÚCLEOS
El modelo de la mecánica cuántica - 2ª parte
Niveles de energía y números cuánticos (continuación)
 omo ya se dijo en el apartado anterior, la
cuantificación pudo se explicada gracias las ideas aplicadas a las órbitas del modelo de Bohr.
omo ya se dijo en el apartado anterior, la
cuantificación pudo se explicada gracias las ideas aplicadas a las órbitas del modelo de Bohr.
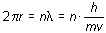
(n = 1.2.3...)
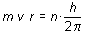
El enfoque de De Broglie fue recogido por la mecánica cuántica,
de modo que estados estacionarios del electrón con energía cuantificada se
corresponden con funciones de ondas
 estacionarias. Un electrón en un átomo se
halla atrapado por la acción del núcleo sin poder salir de su zona de influencia
a menos que reciba energía del exterior. Es como si el electrón estuviera
confinado en una caja. Sus movimientos, que están controlados por la onda
asociada, han de ser tales que correspondan a ondas
estacionarias. Un electrón en un átomo se
halla atrapado por la acción del núcleo sin poder salir de su zona de influencia
a menos que reciba energía del exterior. Es como si el electrón estuviera
confinado en una caja. Sus movimientos, que están controlados por la onda
asociada, han de ser tales que correspondan a ondas
 estacionarias compatibles
con las dimensiones de la caja y con las condiciones que imponen sus límites, lo
que da lugar a una selección
estacionarias compatibles
con las dimensiones de la caja y con las condiciones que imponen sus límites, lo
que da lugar a una selección  1 ...
1 ...
 2 de estados permitidos y, por tanto, a una
secuencia E1 ... En de valores discontinuos que describen de una forma
simplificada los posibles niveles energéticos del electrón dentro de esa caja
imaginaria.
2 de estados permitidos y, por tanto, a una
secuencia E1 ... En de valores discontinuos que describen de una forma
simplificada los posibles niveles energéticos del electrón dentro de esa caja
imaginaria.
El número cuántico principal se representa por la letra n y da idea de la distancia media que separa el electrón del núcleo. Es el número que en una primera aproximación determina la energía de los posibles estados cuánticos del electrón. Toma valores enteros n = 1, 2, 3 ...
El número cuántico secundario se representa por la letra l y está relacionado con la forma geométrica de los orbitales. Desde un punto de vista energético, el número cuántico l describe el estado del electrón en un segundo nivel de refinamiento. Así, cada nivel n se desdobla en otros tantos subniveles l definidos por los valores enteros comprendidos entre 0 y n-1. Este número cuántico permite explicar la llamada estructura fina de los espectros atómicos. En ausencia de campos magnéticos, la energía de un electrón queda determinada por los números cuánticos n y l.El número cuántico magnético se representa por la letra ml y da cuenta de las posibles orientaciones espaciales del movimiento orbital del electrón cuando se le somete a la acción de un campo magnético externo. En tales circunstancias el movimiento electrónico es perturbado por la influencia del campo y cada subnivel se desdobla en tantos otros como valores puede tomar ml, que son todos los números enteros, incluido el cero, comprendidos entre +l y -l; en total son 2l + 1 valores.
El número cuántico de espín se representa por la letra ms y puede tomar dos únicos valores: +1/2 y -1/2. El electrón se comporta como si efectuase un movimiento de giro interno (en inglés spin = giro) con dos posibles sentidos de rotación, a derecha y a izquierda; o más exactamente, el electrón se manifiesta como un minúsculo imán cuya orientación, al aplicar un campo magnético externo, sólo puede ser o paralela (ms = + 1/2) o antiparalela (ms = - 1/2) a la dirección del campo.



