---

1 2

n péndulo simple está formado, en esencia, por un cuerpo de pequeña extensión, como una bola o un disco, que cuelga de un punto fijo a través de un hilo largo de longitud fija (inextensible) y masa despreciable.

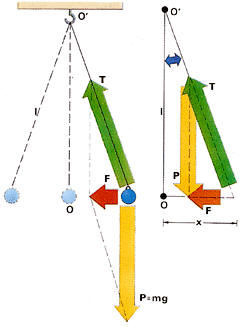
Cuando la desviación x de un péndulo simple es pequeña frente a su longitud, su movimiento resulta ser un movimiento armónico simple

Un estudio dinámico del movimiento del péndulo

El movimiento de un péndulo simple es uno de los muchos movimientos naturales que pueden ser considerados como armónico simples. Para comprobarlo, es preciso efectuar un análisis dinámico del mismo. Las fuerzas que actúan sobre el cuerpo, supuesto aislado, son el peso P y la tensión T del hilo. La suma de ambas, efectuada mediante la composición del triángulo de fuerzas, dará lugar a la fuerza neta o resultante F.

Si el hilo es suficientemente largo, la trayectoria curva de la bola al oscilar de un lado para otro puede considerarse como aproximadamente rectilíneo. Admitiendo tal simplificación, resulta que el triángulo formado por las fuerzas P, T y F es semejante al que forma la línea vertical por el punto de suspensión, la línea horizontal que paralela al techo pasa por el cuerpo, y la línea del hilo. Por tanto, de acuerdo con el teorema de Tales, de semejanza entre triángulos, se tiene:

siendo x la elongación y l la longitud del hilo.

Dado que P = mg, se tiene para la fuerza neta responsable del movimiento:

De acuerdo con la segunda ley de Newton, producirá una aceleración a = F/m, es decir:

(7.18)

en donde el signo - se incluye para recordar que, también en este caso, la fuerza y el desplazamiento tienen signos opuestos.

La expresión de la aceleración es del tipo:

a = - cte · x

Se trata, por tanto, de la aceleración de un movimiento armónico simple. Identificando en este caso las ecuaciones (7.1) y (7.18) resulta:

(7.19)

es decir:

Las fórmulas de la elongación y de la velocidad del M.A.S. son también aplicables al estudio de un péndulo simple, siempre que los ángulos de desviación (con respecto de la vertical) sean pequeños. Para ello basta

1 2

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios