---

1 2 3 4

Cálculo de la posición del centro de gravedad

unto a los procedimientos prácticos existe la posibilidad de determinar, mediante cálculo, la posición del centro de gravedad a través de sus coordenadas.

Las fórmulas que definen las coordenadas xG, yG, zG del c.d.g. para un sólido rígido formado por n partículas son las siguientes:

en donde (x1, y1, z1)...(xn, yn, zn) son las coordenadas de cada una de las partículas que constituye el sistema rígido; p1...pn representa sus pesos respectivos y P el peso total.

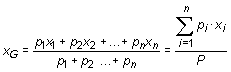
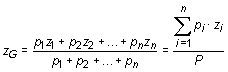
El principio en el que se apoya la deducción de esta forma es análogo al que se emplea en la determinación del punto de aplicación de un sistema de dos fuerzas paralelas y de igual sentido, pues se trata precisamente de determinar ese punto para las fuerzas del peso.

En sistemas no muy extensos en los que la aceleración de la gravedad g es la misma para cualquiera de sus puntos, tras sustituir los pesos por el producto de m por g, es posible sacar factor común g en el numerador de las anteriores fórmulas y cancelarla con la g común del denominador; con lo cual las masas aparecen en las fórmulas en lugar de los pesos.

Las anteriores ecuaciones de las coordenadas del c.d.g. son aplicables estrictamente a cuerpos rígidos que pueden considerarse como agregados discontinuos de partículas. Su generalización a sistemas continuos es posible recurriendo a las matemáticas superiores.

No obstante, si el sólido es homogéneo e irregular, pero puede descomponerse en partes de masa conocida que sí son regulares, es posible entonces sustituir cada parte por su c.d.g. respectivo, que coincidirá con el centro geométrico de esa fracción del cuerpo total. Componiendo las porciones de esos centros de gravedad parciales, según las fórmulas anteriores, es posible determinar entonces el c.d.g. total del sólido homogéneo considerado.

Tomando como ejemplo el sistema de cuerpos que se ilustra en la figura siguiente -en el cual la masa de las uniones entre las esferas se considera despreciable- se pueden aplicar las fórmulas del cálculo del c.d.g. de acuerdo con el siguiente procedimiento general:

1. Se elige un sistema de ejes que pase por el mayor número de puntos máximos posibles, en este caso el que contiene a la base y a la altura del triángulo equilátero.

2. Se establecen las coordenadas de cada uno de los puntos:

siendo I el valor de la longitud del lado.

3. Se aplican ordenadamente las fórmulas del c.d.g.

1 2 3 4

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios