| Natureduca - Portal educativo de ciencia y cultura |

Física
LAS FUERZAS Y EL EQUILIBRIO
Equilibrio bajo las fuerzas del peso - 2ª parte
La estabilidad de los cuerpos apoyados
 n el caso de los cuerpos apoyados, la estabilidad depende
también de la formación de un par de fuerzas entre el peso del cuerpo aplicado
en el c.d.g. y la reacción R del plano que lo soporta en el punto
de apoyo del sólido. El equilibrio será estable cuando al desviarlo de la
posición de equilibrio el par que forma ambas fuerzas haga recuperar al cuerpo
la posición inicial. Será inestable si cualquier pequeño cambio rompe el
equilibrio.
n el caso de los cuerpos apoyados, la estabilidad depende
también de la formación de un par de fuerzas entre el peso del cuerpo aplicado
en el c.d.g. y la reacción R del plano que lo soporta en el punto
de apoyo del sólido. El equilibrio será estable cuando al desviarlo de la
posición de equilibrio el par que forma ambas fuerzas haga recuperar al cuerpo
la posición inicial. Será inestable si cualquier pequeño cambio rompe el
equilibrio.
También los cuerpos apoyados tienden a adoptar una posición tal que permita a su centro de gravedad situarse en el punto más bajo posible. La acción de los pares de fuerza tanto en la recuperación del equilibrio como en la pérdida del mismo está orientada siempre hacia ese objetivo.
El estudio de la balanza como sistema en equilibrio
La balanza de brazos iguales permite la comparación directa de pesos, y puesto que masa y peso (ambos en un mismo lugar de la Tierra) son magnitudes directamente proporcionales, constituye un instrumento apropiado de medida de masas.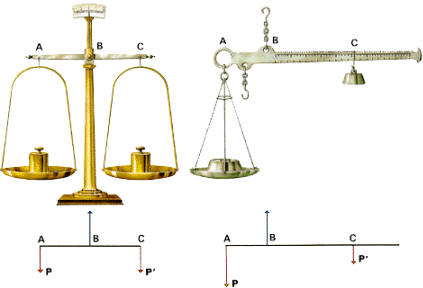
El fundamento de la balanza se
halla en las leyes del equilibrio, y particularmente en la condición general
del equilibrio de rotación que exige que el momento total respecto del punto
de giro sea cero.
La condición de equilibrio de rotación exige que la suma de los momentos de las fuerzas actuantes sea cero. Si se deposita en el otro platillo, mediante un sistema de pesas de valores conocidos, un peso total P' capaz de equilibrar la balanza, los momentos de ambas fuerzas habrán de ser de igual magnitud, es decir:
![]()
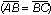 , la condición de equilibrio
equivale a P = P'. Esta relación de igualdad es, entonces, consecuencia de la
igualdad de los momentos y de los brazos de la balanza.
, la condición de equilibrio
equivale a P = P'. Esta relación de igualdad es, entonces, consecuencia de la
igualdad de los momentos y de los brazos de la balanza.La romana es otro tipo de balanza cuyos brazos son desiguales. Consta de un solo platillo, de un peso fijo P que puede desplazarse por una varilla graduada y de un soporte que constituye el punto de giro del sistema. En este caso el equilibrio se logra desplazando el peso fijo a una posición tal que los momentos de la fuerza del peso P' que se trata de medir y del P conocido sean iguales. Considerando el punto de giro B como origen en el cálculo de momentos, en el equilibrio se cumplirá
![]()
![]()
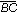 también, el
peso resulta ser directamente proporcional a la distancia, y es posible calibrar
la balanza de modo que las divisiones de la varilla aparezcan graduadas
directamente en unidades de peso.
también, el
peso resulta ser directamente proporcional a la distancia, y es posible calibrar
la balanza de modo que las divisiones de la varilla aparezcan graduadas
directamente en unidades de peso.



