| Natureduca - Portal educativo de ciencia y cultura |

Física
ENERGÍA MECÁNICA Y TRABAJO
Trabajo y transferencia de energía - 4ª parte
Trabajo y energía cinética
 s posible obtener de un modo análogo una fórmula matemática de
esa forma de energía mecánica asociada a la velocidad de los cuerpos. Para ello
es necesario suponer que el cuerpo en cuestión se desplaza sobre un plano
horizontal sin rozamiento bajo la acción de una fuerza constante F.
s posible obtener de un modo análogo una fórmula matemática de
esa forma de energía mecánica asociada a la velocidad de los cuerpos. Para ello
es necesario suponer que el cuerpo en cuestión se desplaza sobre un plano
horizontal sin rozamiento bajo la acción de una fuerza constante F.
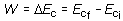
(6.12)
Según la definición de trabajo de una fuerza constante y recordando que de acuerdo con la segunda ley de Newton F = m · a, se tendrá:
W = F · s = m · a · s
Además se sabe que una fuerza constante produce un movimiento rectilíneo uniformemente acelerado, por lo que en la expresión del trabajo el valor de a s dado por esta ecuación, resulta:
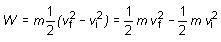
(6.13)
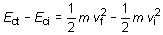
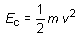
(6.14)

Los trenes de alta
velocidad, como el francés TGV o el español AVE, alcanzan velocidades
superiores a los 240 Km(h. A esa velocidad los efectos de una colisión
serían catastróficos por la enorme cantidad de energía cinética
asociada.
Trabajo y potencia
El trabajo, tal y como ha sido definido, no hace referencia al tiempo que dura el correspondiente proceso de transferencia de energía de un cuerpo a otro.Para dar idea de la rapidez con la que se realiza el trabajo, se introduce la magnitud potencia mecánica; se representa por P y se define como la cantidad de trabajo que puede efectuarse en la unidad de tiempo.
Su expresión matemática viene dada por la ecuación:
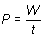
(6.15)
De acuerdo con su definición, expresada en la ecuación (6.15), la unidad de medida de la potencia en el Sistema Internacional será igual a 1 joule/1 segundo. Dicha unidad se denomina watt (W):
1 W = 1 J/1 s
y será, por tanto, la potencia de un agente capaz de realizar un trabajo de 1 joule en un tiempo de 1 segundo. Algunos de los múltiples del watt son utilizados con frecuencia, en especial el kilowatt (1 kW = 103 W) y el megawatt (1 MW = 106 W). El caballo de vapor (CV) es una unidad técnica de potencia que, aun cuando no pertenece al SI, es utilizada frecuentemente en la caracterización de los motores de explosión. Equivale a 735 watts (1 CV = 735 W).



