/natureduca/quimica-los-estados-de-la-materia-el-estado-gaseoso-04

---

1 2 3 4

La teoría cinética: una explicación para las leyes de los gases

as experiencias de Boyle y de otros físicos de la época pusieron caramente de manifiesto que los gases podían comprimirse y expandirse. Pero, ¿cómo explicar estas propiedades que los diferenciaban claramente de los líquidos y los sólidos?

Las ideas de los atomistas griegos influyeron en Boyle de tal manera que propuso dos explicaciones alternativas para el comportamiento de los gases basadas ambas en la hipótesis de que la materia estaba compuesta de partículas indivisibles o átomos.

La primera partía del supuesto de que los átomos estaban en reposo y en contacto mutuo, y explicaba la compresibilidad como consecuencia de una cierta elasticidad de los átomos que podrían comportarse como una especie de muelles blandos. Este modelo estático, sin embargo, no podía explicar la expansibilidad ilimitada de los gases. En cambio, si los átomos no estuvieran ni en reposo ni en contacto mutuo entonces podrían desplazarse rápidamente de un lado a otro en el interior del recipiente, llenando así todo el espacio.

Las ideas tímidamente expuestas por Boyle respecto de la posibilidad de un modelo cinético fueron desarrolladas por el físico suizo Daniel Bernouilli (1700-1782). Según Bernouilli los átomos o corpúsculos de gas, debido a su pequeño tamaño, se encontraban en un enorme número aun en pequeños volúmenes gaseosos. Su movimiento incesante producía choques entre sí y con las paredes del recipiente. Esta innumerable cantidad de impactos de los corpúsculos gaseosos explicaba el efecto observable de la presión del gas y, por tanto, su expansibilidad.

De acuerdo con sus razonamientos, la disminución del volumen del gas restringe el recorrido de los corpúsculos móviles y por tanto, incrementa el número de choques por segundo contra las paredes del recipiente, esto es, aumenta la presión del gas. Estudios teóricos apropiados permitieron a Bernouilli deducir, matemáticamente, la ley de Boyle a partir de estas sencillas ideas. Junto con la explicación del por qué de la ley de Boyle, la teoría cinética de los gases logró, asimismo, la explicación de las leyes de Gay-Lussac.

Además, a partir del significado de la presión del gas según el modelo cinético y de la segunda ley de Gay-Lussac, fue posible encontrar un significado también cinético a la magnitud temperatura. Así cuanto mayor es la temperatura de un gas tanto mayor es la presión que ejerce, es decir, más enérgicos deben ser los impactos de las partículas del gas sobre el interior del recipiente.

Estudios más rigurosos desarrollaron esta idea sencilla sugerida por el físico alemán Rudolph Clausius (1822-1888) y permitieron establecer que la temperatura absoluta de un gas constituye una medida de la energía cinética media de las moléculas del gas en su movimiento de agitación desordenada.

La extensión de la teoría cinética a otros estados de agregación de la materia ha permitido comprender los fenómenos de cambio de estado desde un punto de vista molecular.

Aplicación de la ecuación de estado de los gases

Una cierta masa de nitrógeno ocupa 10 litros a 1 atm de presión y 27 Cº de temperatura. ¿Qué volumen ocupará la misma masa de gas si las condiciones cambian a 2 atm y 207 Cº ¿Cuál sería la presión del gas si las condiciones finales de volumen y temperatura fueran de 20 litros y 27 Cº

La relación entre los valores de las magnitudes P, V y T de un gas en un estado inicial y otro final puede encontrarse aplicando correctamente la ecuación de estado. En todo caso, es preciso recordar que la T que aparece en ella es temperatura absoluta. Si se designa con el subíndice 0 el estado inicial y con el 1 el estado que corresponde a las condiciones de la primera pregunta del problema, se tendrá entonces:

en donde

P0 = 1 atm
V0 = 10 litros
T0 = 27 + 273 = 300 K
P1 = 2 atm
T1 = 207 + 273 = 480 K

luego despejando V1 resulta:

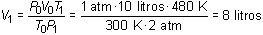
Análogamente y designando con el subíndice 2 el estado que corresponde a las condiciones de la segunda pregunta, resulta:

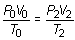
siendo V2 = 20 litros y T2 = T0 = 300 K. Luego:

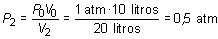
En este caso la transformación se ha efectuado a T = cte, es decir, en las condiciones que recoge la ley de Boyle.

1 2 3 4

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios