/natureduca/quimica-espectros-y-nucleos-espectros-atomicos-01

---

1 2

Espectros de emisión

uando un elemento químico en forma gaseosa o de vapor recibe energía, bien por calentamiento a alta temperatura, bien por una descarga eléctrica de alta tensión, emite luz que puede ser analizada mediante un espectroscopio.

Multitud de observaciones de este tipo fueron realizadas durante el siglo XIX, obteniéndose una secuencia de líneas que resultó ser característica del elemento empleado como fuente de luz. Los espectros de emisión se convirtieron así en métodos de identificación de los elementos y de los átomos que los constituyen, por lo cual se les denomina también espectros atómicos. Hacia 1860 Kirchhoff y Balmer analizando la luz proveniente del Sol mediante un espectroscopio consiguieron demostrar la existencia en su atmósfera de diferentes elementos químicos, entre ellos el hidrógeno.

Espectro de emisión de hidrógeno. La imagen obtenida por un espectroscopio está compuesta por una serie de bandas características de cada elemento químico emisor, en este caso del hidrógeno.

La aplicación del estudio espectroscópico a la determinación de la composición de las sustancias (análisis espectroquímico) se desarrolló rápidamente. Así se consiguió determinar la composición de los meteoritos, y analizando por este procedimiento el vapor de agua mineral se llegó a descubrir la existencia de dos nuevos elementos, el rubidio y el cesio.

El espectro del hidrógeno, por su sencillez, atrajo la atención de diferentes investigadores. Se trataba de una serie formada por quince líneas, que se van juntando cada vez más según se recorre la serie desde la región del rojo hacia la del violeta, y cuyas longitudes de onda pudieron ser medidas con bastante precisión. Estudiando esta serie, J. J. Balmer en 1885 encontró una fórmula que permitía reproducir sus líneas componentes una a una. La sencilla fórmula de Balmer era:

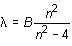
(16.1)

siendo B una constante igual a 3.646 Å y n un número entero que toma el valor 3 para la primera línea (Ha), 4 para la segunda (Hb), 5 para la tercera (Hy) y así sucesivamente. Aun cuando Balmer no dio ninguna explicación a su fórmula, fue capaz de descubrir el orden y la regularidad existente detrás de los datos experimentales.

Algunos años después, Rydberg propuso otra expresión equivalente para la fórmula de Balmer:

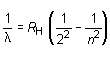
(16.2)

donde RH es la llamada constante de Rydberg cuyo valor es de 109 677,6 cm-1 y n toma los valores 3, 4, 5... La ventaja de esta expresión frente a la de Balmer consistía en sugerir la posibilidad de expresar el inverso de la longitud de onda de una línea dada o número de ondas como la diferencia entre dos términos numéricos T1 y T2:

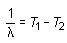
(16.3)

T1 sería fijo e igual a 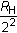y T2 sería variable e igual a 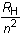; a medida que n aumenta T2 se hace cada vez más pequeño, tendiendo hacia cero, con lo que 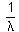tiende hacia T1, que por esta razón se denomina límite de la serie.

Los términos T1 y T2 se denominan términos espectrales y la ecuación (16.3) se conoce como principio de combinación de Rydberg y Ritz. La ecuación de Rydberg y el principio de combinación fueron más tarde generalizados en la forma:

(16.4)

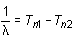
(16.5)

y permitieron describir, además de la de Balmer (n1 = 2; n2 = 3,4,5 ... ) otras series de líneas del espectro del hidrógeno que se conocen por los nombres de sus descubridores. Así, la serie de Lyman, situada en la región del ultravioleta, es descrita por la fórmula de Rydberg cuando se considera n1 = 1 y n2 = 2,3,4 ... En la serie de Paschen n1 = 3 y n2 = 4,5,6 ... ; en la de Brackett n1 = 4 y n2 = 5,6,7... y en la de Pfund n1 = 5 y n2 = 6,7,8. Estas tres últimas series están situadas en la región del infrarrojo.

1 2

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios