| Natureduca - Portal educativo de ciencia y cultura |

Física
MOVIMIENTO VIBRATORIO ARMÓNICO SIMPLE
La cinemática del movimiento armónico simple - 3ª parte
El M.A.S., un movimiento periódico (continuación)
 oherentemente con su definición cinemática, la expresión de la
velocidad v del M.A.S. se obtiene proyectando sobre el eje X la
velocidad vc del movimiento circular auxiliar. Cuando ésta se
considera en forma vectorial, como tangente a la trayectoria con módulo vc
= w · R, su proyección resulta ser:
oherentemente con su definición cinemática, la expresión de la
velocidad v del M.A.S. se obtiene proyectando sobre el eje X la
velocidad vc del movimiento circular auxiliar. Cuando ésta se
considera en forma vectorial, como tangente a la trayectoria con módulo vc
= w · R, su proyección resulta ser:
![]()
![]()
(7.7)
La representación gráfica de la variación de la velocidad v del M.A.S. con el tiempo indica de forma precisa que la rapidez con la que el punto vibrante se mueve sobre la trayectoria es máxima al pasar por el origen O (j = 0 o j = 180) y se hace nula en los extremos ( j = 90 o j = 270), es decir, para t = 0 o t = T/2, y para t = T/4 y t = 3T/4 respectivamente.
Aceleración
El movimiento circular uniforme presenta una aceleración que está relacionada con los cambios en dirección de la velocidad cuando ésta es considerada como un vector. La dirección del vector aceleración es la del radio y su sentido se orienta hacia el centro de la circunferencia trayectoria, siendo su módulo:
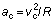
![]()
![]()
(7.8)
Algunas relaciones internas
Entre la elongación, la velocidad y la aceleración de un M.A.S. existen algunas relaciones internas. En el caso de la aceleración la relación con la elongación resulta inmediata. Basta comparar la ecuación (7.8) con la (7.4) para comprobar que, en efecto, a se puede escribir en función de x en la forma:
![]()
(7.9)
Se despeja en (7.4) y (7.7) las funciones seno y coseno respectivas:
![]()
![]()
![]()
![]()
![]()
(7.10)



