---

1 2 3 4 5

Aplicación del estudio de los movimientos circulares

a descripción de un movimiento circular puede hacerse bien en función de magnitudes lineales ignorando la forma de la trayectoria, bien en función de magnitudes angulares. Ambas descripciones están relacionadas entre sí mediante el valor del radio de la circunferencia trayectoria.

Un coche que circula a 72 km/h frena en un instante dado y consigue detenerse tras recorrer una distancia de 40 m. Sus ruedas poseen un radio de 25 cm y se pretende estudiar el movimiento circular de éstas en términos lineales y en términos angulares, calculando su aceleración de frenado y el tiempo que tarda en pararse.

El cálculo de la deceleración del coche se puede efectuar a partir de la fórmula que relaciona las variables a (incógnita) con vo (dato) y s (dato). Dicha expresión es

por tanto:

Dado que el coche termina parándose, la velocidad final v será cero. Antes de sustituir los datos en las fórmulas es preciso expresarles en unidades del Sistema Internacional:

R = 25 cm = 0,25 m

s = 40 m

por tanto,

Si las ruedas no se bloquean, ésta será también la aceleración lineal del movimiento circular descrito por un punto de su superficie, ya que el movimiento de traslación o de avance del coche es el desarrollo del movimiento de rotación de las ruedas. El valor de la aceleración angular correspondiente se podrá calcular dividiendo el anterior valor por el del radio:

El cálculo de a puede efectuarse de un modo alternativo convirtiendo inicialmente los datos en sus correspondientes cantidades angulares y utilizando después las fórmulas del movimiento circular. En tal caso:

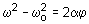
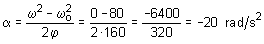
La determinación del tiempo que tarda en pararse puede calcularse a partir de la expresión

en donde a se ha de tomar con su signo, que es, en este caso, negativo:

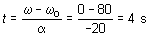
El cálculo del ángulo descrito por uno de sus radios se podrá efectuar a partir de la fórmula

es decir:

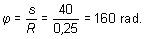
1 2 3 4 5

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios