/natureduca/fisica-movimiento-las-representaciones-cinematicas-03

---

1 2 3 4

Vectores cinemáticos (continuación)

El vector velocidad

l vector velocidad representa la rapidez con la que cambia la posición del cuerpo en el movimiento cuando se considera ésta como un vector. Al igual que en el caso de la velocidad escalar, se podrá definir un vector velocidad media vm en la forma:

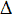o cociente entre el desplazamiento r considerado como un vector y el intervalo de tiempo 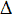t correspondiente. Dicho cociente representa lo que varía el vector posición en la unidad de tiempo. Puesto que 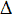t es un número, vm tendrá la misma dirección y sentido que el vector diferencia 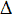r entre las posiciones final r e inicial ro.

Cuando se consideran intervalos de tiempo cada vez más pequeños se advierte que el vector desplazamiento correspondiente tiene una dirección que se acerca cada vez más a la trayectoria, de modo que para intervalos de tiempo suficientemente breves como para ser aceptados como instantes, la dirección de 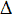r y, por tanto, del vector velocidad será tangente a la trayectoria. El vector velocidad instantánea, expresado mediante la ecuación:

es, por tanto, tangente a la trayectoria.

Además la longitud del vector desplazamiento |dr| al ser éste tan próximo a la trayectoria coincide prácticamente con la correspondiente porción de ella, es decir, con ds. Eso significa que el módulo del vector velocidad instantánea coincide con la velocidad instantánea escalarmente considerada, pues:

En resumen, el vector velocidad instantánea por ser tangente a la trayectoria recoge la dirección u orientación del movimiento en cada instante y por coincidir en módulo con la velocidad escalar contiene, además, información sobre la rapidez del movimiento. Esto demuestra que la descripción en términos de vectores es más complicada que la escalar, pero también más completa.

El vector aceleración

El vector aceleración representa la rapidez con la que el vector velocidad de un cuerpo móvil cambia con el tiempo. Si el intervalo de tiempo considerado es amplio se define el vector aceleración media am en la forma:

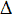o cociente entre la variación que experimenta el vector velocidad durante un intervalo de tiempo t y la amplitud de dicho intervalo. De acuerdo con su definición, el vector aceleración media representa lo que por término medio varía el vector velocidad en cada unidad de tiempo.

Si el intervalo de tiempo 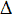t se puede considerar reducido a un instante, el vector aceleración media se convierte en el vector aceleración instantánea a y se expresa en la forma:

donde d representa, de nuevo, una variación muy pequeña.

A diferencia del vector velocidad v, el vector aceleración a es, salvo en los movimientos rectilíneos, no tangente a la trayectoria. Ello es debido a que, de acuerdo con su definición, tiene la misma dirección que v o dv, es decir, que la diferencia de dos vectores velocidad. Dado que tales vectores sucesivos son tangentes a la trayectoria, su diferencia no puede ser también tangente a la trayectoria, a menos que ambos vectores velocidad tengan igual dirección, lo que sucede únicamente en los movimientos rectilíneos.

1 2 3 4

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios