/natureduca/fisica-movimiento-las-representaciones-cinematicas-01

---

1 2 3 4

Introducción

a representación gráfica de un movimiento y de sus características permite extraer una información valiosa sobre dicho movimiento.

La trayectoria es una primera descripción gráfica del movimiento; en ella no se recoge (explícitamente) la variable tiempo, sino que se representa únicamente las posiciones del punto móvil, o lo que es lo mismo, la relación entre sus coordenadas a lo largo del movimiento. Es, por tanto, una gráfica espacial.

Las gráficas en las que se refleja la variación de diferentes magnitudes con respecto al tiempo son gráficas temporales y por sí mismas proporcionan una buena descripción de las características del movimiento considerado. En todas ellas el tiempo t se representa en el eje horizontal o de abscisas y la magnitud cinemática elegida -como el espacio s, la velocidad v o la aceleración a- se representa en el eje vertical o de ordenadas. La variación con respecto al tiempo de cada una de estas magnitudes da lugar a la correspondiente gráfica o diagrama cinemático.

Gráficas espacio-tiempo (s-t)

La gráfica s-t es la gráfica cinemática fundamental, pues representa la relación entre las dos variables básicas en todo movimiento. El espacio s, medido sobre la trayectoria, podría identificarse con el resultado de la lectura del cuentakilómetros de una moto que describiera la trayectoria considerada y el tiempo t sería el resultado de la correspondiente lectura de un cronómetro.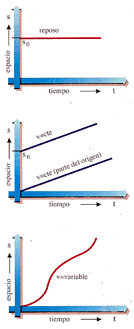

Las gráficas espacio- tiempo representan la variación del espacio medido sobre la trayectoria con respecto al tiempo. Las rectilíneas y oblicuas representan velocidad constante y las curvilíneas corresponden a velocidad variable

La interpretación de una gráfica s-t se efectúa a través del significado de su pendiente. La pendiente m de una gráfica constituye una medida de su inclinación y viene dada por el cociente entre una variación de la magnitud representada en ordenadas y la variación que le corresponde de la magnitud representada en abcisas. Es, por tanto, el ritmo de variación de una variable con respecto a la otra. En el caso de la gráfica s-t, la expresión de la pendiente será entonces del tipo:

que es precisamente la velocidad.

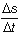
Así, una gráfica s-t que sea una recta paralela al eje horizontal o de tiempos indica que no existe movimiento; el móvil se encuentra parado a una distancia so del origen o línea de salida y no existe variación de s con respecto de t. Una recta oblicua que pasa por el origen indica que s varía con t y, además, que lo hace a un ritmo constante, pues la pendiente es siempre la misma.

Se trata en este caso de un movimiento de velocidad constante en el cual el espacio recorrido es directamente proporcional al tiempo empleado en recorrerlo. Si la recta corta al eje s a una distancia so está coordenada representa la distancia que separa al móvil del origen 0, medida sobre la trayectoria, en el instante inicial. Una gráfica s-t curvilínea, o de pendiente variable, representará un movimiento de velocidad variable en el tiempo.

Aun cuando en la gráfica s-t se represente el espacio, no es una gráfica espacial, es decir, no se trata de algo que pueda verse durante el movimiento, sino de una representación matemática que permite visualizar la forma en la que las variables s y t están relacionadas.

1 2 3 4

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios