/natureduca/fisica-estatica-de-fluidos-hidrostatica-03

---

1 2 3

El principio de Pascal y sus aplicaciones (continuación)

Aplicación del principio de Pascal

l elevador hidráulico de un garaje funciona mediante una prensa hidráulica conectada a una toma de agua de la red urbana que llega a la máquina con una presión de 5 · 105 N/m2.

Si el radio del émbolo es de 20 cm y el rendimiento es de un 90 %, determinar cuál es el valor en toneladas de la carga que como máximo puede levantar el elevador.

De acuerdo con el principio de Pascal:

p1 = p2

que para una prensa hidráulica se transforma en:

En este caso el dato que correspondería al émbolo pequeño de la prensa se facilita en forma de presión, de modo que combinando las ecuaciones anteriores se tiene:

ó 

Como el rendimiento es del 90 % el valor efectivo de la carga máxima expresado en newtons será:

Una tonelada métrica equivale al peso de un cuerpo de 1 000 kg de masa, es decir:

luego:

El principio de los vasos comunicantes

Si se tienen dos recipientes comunicados y se vierte un líquido en uno de ellos en éste se distribuirá entre ambos de tal modo que, independientemente de sus capacidades, el nivel de líquido en uno y otro recipiente sea el mismo. Éste es el llamado principio de los vasos comunicantes, que es una consecuencia de la ecuación fundamental de la hidrostática.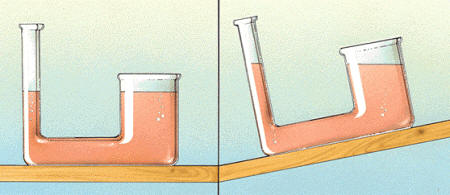

En los vasos comunicantes el líquido alcanza la misma altura en todas las ramas, independientemente del plano horizontal o inclinado sobre el que se asienten.

Si se toman dos puntos A y B situados en el mismo nivel, sus presiones hidrostáticas han de ser las mismas, es decir:

luego si pA = pB necesariamente las alturas hA y hB de las respectivas superficies libres han de ser idénticas hA = hB.

Si se emplean dos líquidos de diferentes densidades y no miscibles, entonces las alturas serán inversamente proporcionales a las respectivas densidades. En efecto, si pA = pB, se tendrá:

(5.7)

Esta ecuación permite, a partir de la medida de las alturas, la determinación experimental de la densidad relativa de un líquido respecto de otro y constituye, por tanto, un modo de medir densidades de líquidos no miscibles si la de uno de ellos es conocida.

1 2 3

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios