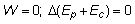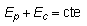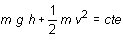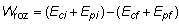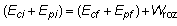---

1 2 3

Conservación de la energía mecánica

uando se consideran únicamente transformaciones de tipo mecánico, es decir, cambios de posición y cambios de velocidad, las relaciones entre trabajo y energía se convierten de hecho en ecuaciones de conservación, de modo que si un cuerpo no cede ni toma energía mecánica mediante la realización de trabajo, la suma de la energía cinética y de la energía potencial habrá de mantenerse constante. Eso es lo que también se deduce de la ecuación (6.16). En efecto, si

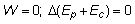
Pero decir que la suma Ep + Ec no varía entre los estados inicial y final equivale a afirmar que su energía mecánica total se mantiene constante a lo largo del movimiento:

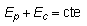
El sistema podrá variar su energía cinética y su energía potencial y cambiar por tanto de velocidad y de posición, con la única restricción de que la suma de aquéllas se mantenga constante. Así, un aumento en el término de energía cinética debe llevar asociado la disminución correspondiente de la energía potencial para que en conjunto nada cambie. Este sería el caso de un péndulo ideal sin rozamientos; si se le eleva a una altura dada y se le suelta a continuación, el péndulo oscilará indefinidamente, ganando velocidad a medida que pierde altura y posteriormente ganando altura a medida que pierde velocidad. Esta transformación continua e indefinida de energía potencial en energía cinética y viceversa es una consecuencia de la ecuación de conservación:

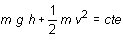
La conservación de la energía mecánica explica el principio empírico formulado por Galileo y defendido posteriormente por Leibniz según el cual un cuerpo que cae desde una altura dada adquiere una velocidad lo suficientemente grande como para, tras rebotar en el suelo, elevarse de nuevo hasta la altura inicial. Suponiendo despreciables las pérdidas de energía mecánica, por el choque contra el suelo y por rozamiento con el aire, la energía mecánica total inicial se ha de conservar. Al principio sólo es potencial; al llegar al suelo se ha transformado completamente en energía cinética, la cual, tras el choque, va convirtiéndose progresivamente en potencial conforme el cuerpo gana altura, hasta recuperar la posición inicial.

La conservación de la energía y el trabajo por rozamiento

La presencia de fuerzas de rozamiento impide la aplicación de la conservación de la energía mecánica, dado que en tales condiciones esta forma de energía disminuye durante el movimiento. No obstante, es posible recurrir a un principio más general, cual es el de la conservación de la energía total, pues aunque la energía mecánica se pierda como tal por efecto del rozamiento, no se destruye, sino que se invierte precisamente en realizar un trabajo en contra de esas fuerzas de fricción.

Expresando el anterior razonamiento en forma matemática, para dos estados inicial y final cualesquiera del cuerpo en movimiento, se tiene la siguiente expresión:

que significa precisamente que la pérdida o disminución - DE de la energía mecánica se ha invertido en la realización de trabajo contra el rozamiento. Recordando que la energía mecánica total E es suma de un término de energía cinética Ec más otro de energía potencial Ep, la anterior expresión puede escribirse en la forma:

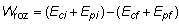
o también:

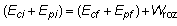
El trabajo por rozamiento Wroz se convierte ahora en el término que permite ajustar el balance de energía mecánica entre las posiciones inicial y final del cuerpo. Representa, por tanto, la energía mecánica disipada.

Aceptando la simplificación consistente en suponer constantes las fuerzas de rozamiento, es posible expresar Wroz de acuerdo con la definición de trabajo en la forma:

Wroz = Froz · s

siendo s el desplazamiento o longitud recorrida por el cuerpo entre las posiciones inicial y final.

La ecuación de conservación de la energía permite entonces calcular la fuerza de rozamiento Froz, supuesta constante, sin más que despejarla de ella:

Froz = [(Eci + Epi) - (Ecf + Epf)]/s

Así, pues, mediante procedimientos energéticos es posible calcular la energía mecánica perdida por el cuerpo; dividiendo por el desplazamiento, se tiene una estimación de la fuerza de rozamiento supuesta constante.

1 2 3

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios