---

1 2 3 4 5

La ecuación de una onda

l movimiento ondulatorio puede expresarse en forma matemática mediante una ecuación que describa un movimiento vibratorio avanzando por un medio.

Para ello es preciso partir de la ecuación que define la oscilación del foco u origen de la perturbación. Si el movimiento es armónico simple su ecuación correspondiente será:

Y = A · sen w t

o también

Y = A · sen (2pft)

Donde la elongación se representa, en este caso, por la letra Y, pues en ondas transversales, como sucede en las cuerdas, equivale a una altura.

Dado que la perturbación avanza a una velocidad v, en recorrer una distancia r

Eso significa que el estado de perturbación de cualquier punto P situado a una distancia r del foco O coincidirá con el que tenía el foco t' segundos antes. Se trata de un tiempo de retardo que indica en cuánto se ha retrasado la perturbación al llegar a P respecto del foco.

Por tanto, si en la ecuación de la elongación que describe la situación del foco, se cambia t por t-t' se obtiene una ecuación que describe el estado de perturbación del punto P:

Dado que t y r hacen referencia a instantes genéricos y distancias genéricas respecto del foco O, la anterior ecuación describe el estado de perturbación del medio, medido por la altura Y en cualquier punto y en cualquier instante, lo que constituye una buena descripción matemática de una onda armónica.

El argumento de la función seno correspondiente puede expresarse también en la forma

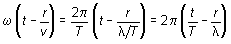
dado que w= 2p/T y v = l/T; lo cual permite escribir la ecuación de ondas en función de sus parámetros o constantes características, tales como la amplitud A, el periodo T y la longitud l.

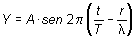
La ecuación de onda recibe también el nombre de función de onda y puede referirse a una perturbación genérica que no consista precisamente en una altura, si se sustituye Y por la letra griega Y que designa la magnitud de la perturbación. En tal caso, la función de onda toma la forma

en donde Y puede representar la alteración, con el tiempo, de propiedades físicas tan diversas como una densidad, una presión, un campo eléctrico o un campo magnético, por ejemplo, y su propagación por el espacio.

1 2 3 4 5

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios