/natureduca/fisica-ondas-y-particulas-principio-de-indeterminacion-03

---

1 2 3

La relación de indeterminación energía-tiempo

l principio de indeterminación de Heisenberg puede aplicarse también al par de variables energía-tiempo en la forma:

expresión que, como en el caso de las variables posición-cantidad de movimiento, indica un compromiso entre las precisiones con las que pueden medirse E y t. Una precisión elevada en la medida del tiempo lleva consigo una imprecisión considerable en la medida de la energía E y viceversa.

Una deducción simplificada de esta nueva relación de indeterminación puede hacerse para los procesos de emisión de radiación por un átomo en la forma siguiente. De acuerdo con la ecuación de Planck E = hf y dado que h es una constante, se podrá expresar en términos de imprevisiones en la forma ∆E = h∆f. Pero f = 1/T y T es el período de la onda electromagnética correspondiente, se trata por tanto de un tiempo, por lo que ∆f = 1/∆t, es decir, ∆E · ∆t = h.

Una de las consecuencias de esta relación la constituye la anchura de líneas de los espectros de emisión o de absorción de radiación por los átomos. Cuando un átomo recibe energía de ciertas características, se excita desprendiendo a continuación ese exceso de energía en forma de radiación. El tiempo que transcurre entre la excitación y la emisión es del orden de ∆t = 10 8 s lo cual, aplicando la relación: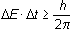

da lugar a una indeterminación en la frecuencia de la radiación emitida de ∆f = 1,6 · 107 Hz. Ello se traduce en que las líneas del espectro correspondiente aparecen como bandas que no corresponden a una frecuencia única, sino a una gama de frecuencias de anchura ∆f.

Aplicación de la relación de incertidumbre

Comparar, de acuerdo con el principio de Heisenberg, las indeterminaciones en las velocidades de un electrón y de un protón en el supuesto de que estuvieran ambos confinados en una caja cuya dimensión máxima fuera de 10 Å.

(Tómense las masas del protón y del electrón como mp = 1,672 · 10^-27 kg; me = 9,108 · 10^-31 kg y la constante de Planck h = 6,625 · 10^-34 J · s.)

La relación de indeterminación posición-cantidad de movimiento puede escribirse en la forma:

Si una partícula se mueve en esa caja, la indeterminación en la posición será como máximo igual al valor del recorrido más largo que puede efectuar la partícula dentro de la caja, es decir, ∆x = 10 Å = 10^-9 m. Admitiendo que la masa de cada una de las partículas está bien determinada y es constante en su movimiento dentro de la caja, la indeterminación en la cantidad de movimiento

p = mv se puede escribir como:

∆p = m · ∆v

Sustituyendo en la relación de indeterminación, resulta:

es decir:

Nótese la magnitud de los errores que se producirían al intentar medir la velocidad de ambas partículas. El hecho de que estén confinadas en un pequeño espacio, con su posición por tanto bien determinada, hace que el error en la variable v sea considerable.

1 2 3

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios