---

1 2 3

El enfoque cinemático frente al dinámico

uando se comparan las dos ecuaciones de la página anterior:

 

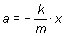
se comprueba que las características del M.A.S. resultante están relacionadas con las propiedades del oscilador, propiedades definidas por la constante elástica del muelle y por la masa del cuerpo. Así, igualando los respectivos coeficientes de la variable x en ambas ecuaciones resulta:

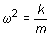
(7.12)

El periodo T y, por tanto, la frecuencia f de un movimiento armónico simple depende únicamente de dos factores: la masa del cuerpo en vibración y la constante elástica de la fuerza que origina el movimiento. Cuanto mayor sea la constante elástica, más intensa será la fuerza recuperadora, lo cual se traduce en un periodo T de vibración menor. Sin embargo, aumentar la masa m equivale a aumentar la inercia u oposición al movimiento, lo que da lugar a que el periodo T sea en tal caso mayor.

Aplicación de la dinámica del oscilador armónico

El estudio dinámico del oscilador supone el manejo simultáneo de las características de la fuerza (en particular de su constante elástica k), de las características del cuerpo, a través de su masa m, y de las características del movimiento resultante, tales como posición, velocidad o aceleración.

Cuando a un muelle se le somete a una carga de 50 g se alarga 2 cm. A ese mismo muelle se le cuelga un cuerpo de 300 g y se efectúa sobre él una tracción hacia abajo. Al soltar el cuerpo, el sistema realiza un M.A.S. de 10 cm de amplitud.

Se trata de determinar:

a) la constante elástica k del muelle;

b) el periodo de oscilación;

c) la velocidad máxima del cuerpo;

d) la velocidad y la aceleración cuando el cuerpo se halla 5 cm por debajo de la posición de equilibrio.

a) La operación preliminar de carga permite averiguar la constante elástica k del muelle. Dado que Fe = k · x se tiene:

Expresando todas las cantidades en unidades SI y sustituyendo se tiene:

b) El periodo de vibración depende de las características del oscilador definidas por su masa m y su constante k en la forma:

es decir:

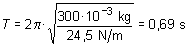
donde la masa empleada ahora corresponde a la del cuerpo que efectúa la oscilación que se pretende estudiar.

c) La velocidad del oscilador alcanza el valor máximo para cos wt = 1, es decir:

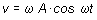
Sustituyendo las cantidades correspondientes expresadas en unidades SI se tiene:

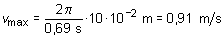
d) Puesto que lo que se da es el valor de la elongación y no del tiempo, será necesario emplear las expresiones de v y de a en función de x:

Sustituyendo resulta para la velocidad:

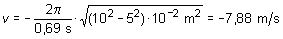
El signo + se aplica cuando el punto se aleja del origen o punto de equilibrio O y el signo - cuando se acerca a él. En este caso, al estar el cuerpo por debajo de dicho punto, la fuerza recuperadora le llevará hacia él, de ahí que se tome la determinación negativa de la raíz cuadrada.

Y, análogamente, se tiene para la aceleración:

El signo - del valor de la aceleración refleja el hecho de que la fuerza recuperadora que la origina se dirige siempre hacia el punto de equilibrio O.

1 2 3

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios