| Natureduca - Portal educativo de ciencia y cultura |

Física
EL ESTUDIO DE LOS MOVIMIENTOS
Los movimientos rectilíneos - 5ª parte
Movimiento de caída libre (continuación)
 a ley de que los cuerpos caen en el vacío con una aceleración
que es la misma para todos ellos e independiente de sus pesos respectivos fue
establecida por Galileo Galilei y comprobada mediante un experimento
espectacular. Desde lo alto de la torre inclinada de la ciudad italiana de Pisa,
y en presencia de profesores y alumnos de su Universidad, Galileo soltó a la vez
dos balas de cañón, una de ellas diez veces más pesada que la otra. Con este
experimento Galileo planteaba una pregunta directamente a la naturaleza y ella
se encargó de responder que, dentro del error experimental, ambos cuerpos, a
pesar de las diferencias entre sus pesos, caen a la vez, es decir, recorren el
mismo espacio en el mismo tiempo.
a ley de que los cuerpos caen en el vacío con una aceleración
que es la misma para todos ellos e independiente de sus pesos respectivos fue
establecida por Galileo Galilei y comprobada mediante un experimento
espectacular. Desde lo alto de la torre inclinada de la ciudad italiana de Pisa,
y en presencia de profesores y alumnos de su Universidad, Galileo soltó a la vez
dos balas de cañón, una de ellas diez veces más pesada que la otra. Con este
experimento Galileo planteaba una pregunta directamente a la naturaleza y ella
se encargó de responder que, dentro del error experimental, ambos cuerpos, a
pesar de las diferencias entre sus pesos, caen a la vez, es decir, recorren el
mismo espacio en el mismo tiempo.
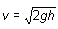
Aplicación del estudio de los movimientos de caída
Los movimientos de los cuerpos sometidos a las fuerzas del peso constituyen un ejemplo de movimientos de aceleración constante e igual a 9,8 m/s2 cuando se desprecia la acción del rozamiento. Si el movimiento es de descenso dicho valor se tomará como positivo, pues el cuerpo gana velocidad con el tiempo. Si el cuerpo asciende como consecuencia de un impulso o velocidad inicial, su velocidad disminuye con el tiempo y la aceleración de la gravedad se considerará negativa. La determinación de magnitudes cinemáticas tales como velocidad, altura o tiempo se podrán determinar, en tales casos, con la ayuda de las fórmulas correspondientes.
Así, si se lanza verticalmente hacia arriba una bola de acero con una velocidad inicial de 10 m/s cabe preguntarse a qué altura llegará. Se dispone del valor de vo = 10 m/s, del valor de la aceleración g = 9,8 m/s y también del valor de la velocidad final, puesto que la bola, al perder progresivamente velocidad, terminará por pararse, iniciando a continuación un movimiento de descenso. Se trata entonces de identificar una fórmula del movimiento uniformemente decelerado que relacione las magnitudes v (dato), g (dato) y h (incógnita). Dicha expresión es:
![]()
Despejando h y sustituyendo se tiene:
![]()
El tiempo que ha empleado el cuerpo en alcanzar esta altura máxima puede, asimismo, determinarse a partir de los datos iniciales. Se trata en este caso de identificar una fórmula que relacione v, g y t, siendo v y g conocidas; dicha expresión es
![]()
Despejando t y sustituyendo resulta:
![]()
Otra cuestión de interés en este tipo de movimientos es averiguar con qué velocidad volverá a caer. En el punto más alto de su trayectoria el cuerpo carece de velocidad, de modo que iniciará el movimiento de descenso partiendo del reposo, vo = 0. El espacio que recorre al subir es el mismo que el que recorre al bajar, de modo que, haciendo uso nuevamente de la expresión:
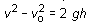
pero considerando ahora g con valor positivo resulta:
![]()
v2 = 2 · 9,8 · 5,1 = 10 m/s
En ausencia de rozamientos, los movimientos de ascenso y descenso son perfectamente simétricos, de modo que el cuerpo emplea el mismo tiempo en subir que en bajar, y vuelve al punto de lanzamiento con idéntica velocidad con la que partió de él.
Es, asimismo, interesante saber calcular la altura que alcanzaría en la mitad del tiempo de ascenso. Como paso previo se han de identificar con claridad las nuevas incógnitas, así como los datos disponibles. Se conoce el tiempo t = 1,0/2, la aceleración g = 9,8 m/s2 y la velocidad inicial vo = 10,0 m/s y se desea averiguar la altura h; la ecuación que relaciona tales magnitudes es:
![]()
Sustituyendo los valores numéricos se obtiene:
![]()
De acuerdo con este resultado en la primera mitad del tiempo total, el cuerpo recorre más de la mitad del espacio total, lo que indica que el movimiento no es uniforme.



