---

1 2

Trabajo de una fuerza variable

na situación más general, y por lo tanto más compleja, es aquélla en que la fuerza no es constante, sino que varía con el tiempo, ya sea en intensidad, ya sea en dirección y sentido.

La ecuación 6.4 sugiere que si se construye una gráfica que represente la variación del valor de la componente útil representada en ordenadas, con el desplazamiento representado en abscisas, el área comprendida entre la gráfica y el eje de abcisas coincidirá con el trabajo W realizado por la fuerza a lo largo del desplazamiento 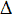s.

En el caso de una fuerza constante Ft no varía con s y la propiedad anterior resulta inmediata; se trata de calcular el área de un rectángulo cuya base es 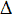s y cuya altura es Ft que, de acuerdo con (6.4), coincide con W. En el caso de una fuerza variable siempre es posible dividir el desplazamiento total en desplazamientos elementales lo suficientemente cortos como para aceptar que la fuerza a lo largo de cada uno de ellos es aproximadamente constante, aun cuando cambie su valor de uno a otro. La superficie bajo la gráfica fuerza útil-desplazamiento queda entonces descompuesta en una serie de rectángulos de altura variable, la suma de cuyas áreas coincidirá prácticamente con el área total.

Expresando lo anterior en términos de fuerzas y trabajo, resulta:

es decir:

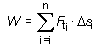
(6.6)

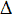Esta igualdad aproximada será tanto más cierta cuanto más pequeños sean los intervalos s elementales en los que se ha descompuesto el desplazamiento total s. A partir de la gráfica Ft - s es posible entonces, midiendo áreas, calcular el trabajo de una fuerza variable.

El trabajo como producto de vectores

Según la definición de trabajo W de una fuerza constante: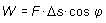

El hecho de que tanto la fuerza como el desplazamiento pueden ser considerados en forma vectorial sugiere la posibilidad de expresar el trabajo de modo que ambas magnitudes aparezcan en la fórmula como vectores.

El vector desplazamiento une las posiciones inicial y final del punto de aplicación de la fuerza y se representa mediante el símbolo Dr. La fuerza vectorialmente considerada forma con el vector desplazamiento un ángulo j. Es posible representar entonces el trabajo en la forma:

cuyo significado es:

Este producto de vectores que equivale al producto del módulo del primer vector por el módulo del segundo, por el coseno del ángulo que forman, se denomina producto escalar, porque a pesar de ser un producto de vectores su resultado es un escalar. Para dos vectores a y b cualesquiera se define el producto escalar a · b en la forma:

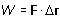
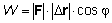
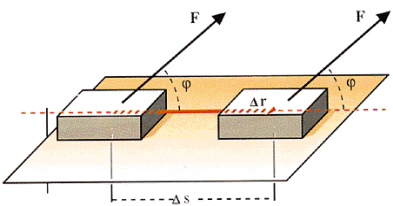
Podemos representar el trabajo como un producto escalar de dos vectores a.b = |a|.|b|.cos φ

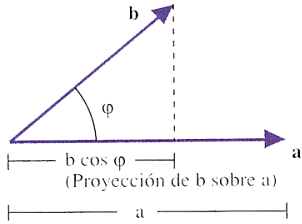
a.b representa el producto del módulo de a por la proyección de b sobre él.

1 2

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios